题目内容
【题目】如图,在△ABC中,∠B=30°,∠C=45°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E。若DE=1,则BC的长为( )

A.2+![]() B.
B.![]() C.
C.![]() D.3
D.3
【答案】A
【解析】
如图,过点D作DF⊥AC于F,由角平分线的性质可得DF=DE=1,在Rt△BED中,根据30度角所对直角边等于斜边一半可得BD长,在Rt△CDF中,由∠C=45°,可知△CDF为等腰直角三角形,利用勾股定理可求得CD的长,继而由BC=BD+CD即可求得答案.
如图,过点D作DF⊥AC于F,
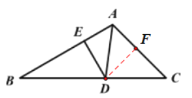
∵AD为∠BAC的平分线,且DE⊥AB于E,DF⊥AC于F,
∴DF=DE=1,
在Rt△BED中,∠B=30°,
∴BD=2DE=2,
在Rt△CDF中,∠C=45°,
∴△CDF为等腰直角三角形,
∴CF=DF=1,
∴CD=![]() =
=![]() ,
,
∴BC=BD+CD=![]() ,
,
故选A.

练习册系列答案
相关题目








