Question

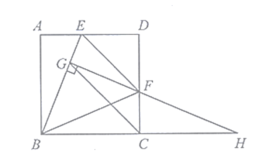
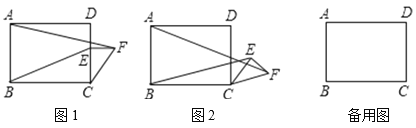
【题目】如图，已知在△ABC中，，，，点E为AB的中点，D为BC边上的一动点，把△ACD沿AD折叠，点C落在点F处，当△AEF为直角三角形时，CD的长为__________．

Answer 1

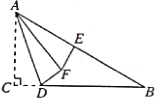
【答案】2或

【解析】

本题以三角形为基础，考查内容包含中点的用法，可立刻推边等；动点图形翻折问题，可得到角等以及边等，解答本题需以题目要求直角三角形为前提，采取分类讨论方法，通过构造辅助线、假设未知数并结合勾股定理求解．

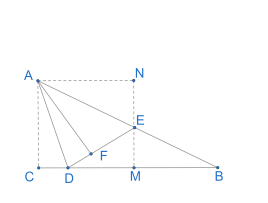
（1）当∠AFE=90°时

作EM⊥BC垂足为M.，作AN⊥ME于N，如下图所示：

∵∠C=∠EMB=90°

∴EM∥AC

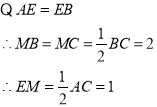
∴∠C=∠CMN=∠N=90°

∴四边形ACMN是矩形

∵AC=CM=2

∴四边形ACMN是正方形

在RT△ABC中，∵AC=2,BC=4

∴AB= ，AE=

在RT△AFE中，∵AE= ，AF=AC=2

∴FE=1

设CD=FD=x，在RT△EDM中，∵DE=1+x，EM=1，DM=2-x

∴

∴CD=

（2）当∠AFE=90°时，如下图所示

∵∠AFD=90°

∴F,E,D三点共线

在RT△AFE中，∵AE= ，AF=AC=2

∴EF=1

又∵DE=1

∴EF=ED

又∵EA=EB，∠AEF=∠BED

所以△AFE△BDE(SAS)

∴∠BDE=∠AFE=90°

故四边形AFCD是矩形

又∵AF=AC

所以四边形AFCD是正方形

∴CD=AC=2