题目内容
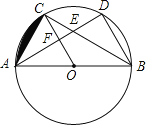
【题目】如图，若
内一点
满足
，则点为的布洛卡点，三角形的布洛卡点由法国数学家和数学教育家克洛尔于1816年首次发现，但他的发现并未被当时的人们所注意．1875年，布洛卡点被一个数学爱好者法国军官布洛卡重新发现，并用他的名字命名．问题：已知等腰直角三角形
中，
．若
为
的布洛卡点，
，则
的值为（ ）
A.10B.
C.
D.
【答案】B
【解析】
通过证明△DQF∽△FQE，可得
，可求FQ，EQ的长，即可求解．
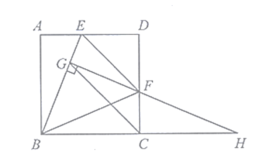
如图，
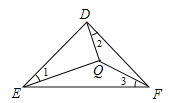
在等腰直角三角形△DEF中，∠EDF=90°，DE=DF，∠1=∠2=∠3，
∵∠1+∠QEF=∠3+∠DFQ=45°，
∴∠QEF=∠DFQ，且∠2=∠3，
∴△DQF∽△FQE，
∴，
∵DQ=2，
∴FQ=
，EQ=4，
∴EQ+FQ=4+，
故选：B．
练习册系列答案
阅读快车系列答案
相关题目
【题目】王老师从本校九年级质量检测的成绩中随机地抽取一些同学的数学成绩做质量分析，他先按照等级绘制这些人数学成绩的扇形统计图，如图（1）所示，数学成绩等级标准见表1，又按分数段绘制成绩分布表，如表2，
表1
等级 | 分数x的范围 |
A | a≤x≤100 |
B | 80≤x＜a |
C | 60≤x＜80 |
D | 0≤x＜60 |
表2
分数段 | x＜60 | 60≤x＜70 | 70≤x＜80 | 80≤x＜90 | 90≤x≤100 |
人数 | 5 | 10 | m | 12 | n |
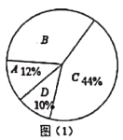
分数段为90≤x≤100的n个人中，其成绩的中位数是95分．
根据以上信息回答下面问题：
（1）王老师抽查了多少人？m、n的值分别是多少；
（2）小明在此考试中得了95分，他说自己在这些考试中数学成绩是A等级，他说的对吗？为什么？
（3）若此次测试数学学科普高的预测线是70分，该校九年级有900名学生，求数学学科达到普高预测线的学生约有多少人？
