题目内容
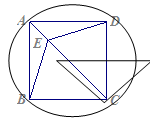
已知:如图,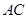 为正方形
为正方形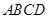 的对角线,
的对角线,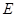 为
为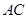 上一点,联结
上一点,联结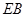 ,
,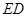 ,当
,当 时,
时,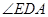 的度数为( )
的度数为( )
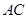 为正方形
为正方形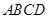 的对角线,
的对角线,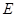 为
为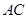 上一点,联结
上一点,联结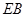 ,
,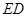 ,当
,当 时,
时,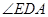 的度数为( )
的度数为( )
| A.54° | B.27° |
| C.36° | D.18 |
D
由ABCD是正方形得∠DAC=45°,又由∠BED=126°得∠DEC=63°,外角等于相邻内角的和而得.
解:∵ABCD是正方形,
∴∠DAC=45°,
∵∠BED=126°,
∴∠DEC=63°,
∴∠EDA=18°.
故选D.
本题考查了正方形的性质,从性质出发利用角平分线平分直角,外角等于相邻内角的和而得.
解:∵ABCD是正方形,
∴∠DAC=45°,
∵∠BED=126°,
∴∠DEC=63°,
∴∠EDA=18°.
故选D.
本题考查了正方形的性质,从性质出发利用角平分线平分直角,外角等于相邻内角的和而得.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
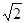 ,则△CEF的周长为
,则△CEF的周长为

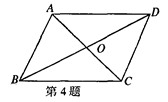

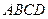 中,
中,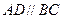 ,
,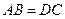 ,
,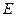 为
为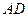 中点,连接
中点,连接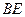 ,
,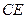 .
.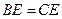 ;
;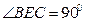 ,过点
,过点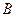 作
作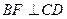 ,垂足为点
,垂足为点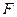 ,交
,交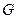 ,连接
,连接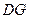 .
.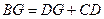 .
.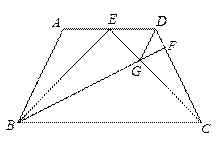
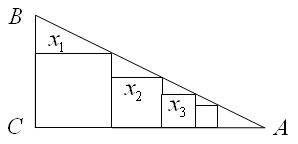
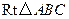 中,
中,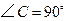 ,
,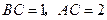 ,把边长分别为
,把边长分别为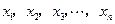 的
的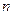 个正方形依次放入
个正方形依次放入 中,请回答下列问题:
中,请回答下列问题: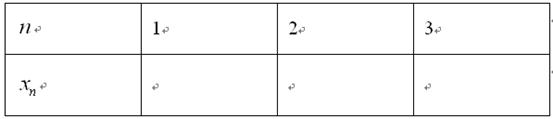
 ;
;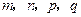 是正整数,且
是正整数,且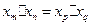 ,试判断
,试判断