题目内容
【题目】为了丰富学生课余生活,某区教育部门准备在七年级开设兴趣课堂.为了了解学生对音乐、书法、球类、绘画这四个兴趣小组的喜爱情况,在全区进行随机抽样调查,并根据收集的数据绘制了下面两幅统计图(信息不完整),请根据图中提供的信息,解答下面的问题:
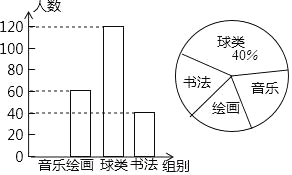
(1)此次共调查了多少名同学?
(2)将条形图补充完整,并计算扇形统计图中音乐部分的圆心角的度数
(3)如果该区七年级共有2000名学生参加这4个课外兴趣小组,而每名教师最多只能辅导本组的20名学生,则绘画兴趣小组至少需要准备多少名教师?
【答案】(1)300名;(2)补图见解析;96°;(3)需准备20名教师辅导.
【解析】
(1)根据球类人数及其所占百分比可得总人数;(2)根据各组人数之和等于总人数求得音乐人数,据此可补全条形图;再用360°乘以音乐人数所占比例可得圆心角度数;(3)总人数乘以样本中绘画人数所占比例,再除以20即可得.
解:(1)此次调查的学生人数为120÷40%=300(名);
(2)音乐的人数为300﹣(60+120+40)=80(名),
补全条形图如下:

扇形统计图中音乐部分的圆心角的度数为360°×![]() =96°;
=96°;
(3)60÷300×2000÷20=20.
∴需准备20名教师辅导.

【题目】2018年俄罗斯世界杯组委会对世界杯比赛用球进行抽查,随机抽取了100个足球,检测每个足球的质量是否符合标准,超过或不足部分分别用正、负数来表示,记录如表:
与标准质量的差值(单位:克) | ﹣4 | ﹣2 | 0 | 1 | 3 | 6 |
个数 | 10 | 13 | 30 | 25 | 15 | 7 |
(1)平均每个足球的质量比标准质量多还是少?用你学过的方法合理解释;
(2)若每个足球标准质量为420克,则抽样检测的足球的总质量是多少克?
【题目】随着地面公交和共享单车的发展,“公交车+单车”的方式已成为很多市民出行的选择。小明放学后从寿春中学出发,先乘坐公交车,根据路面交通的拥堵的实际情况,灵活决定在离家较近的A、B、C、D、E中的某一公交站下车,再骑共享单车回家,设他乘公交车的时间y1(单位:分钟)与下车站点到学校距离x(3≤x≤5)(单位:千米)之间函数关系为y1=2x+2,小明骑单车的时间y2(单位:分钟)与x(3≤x≤5)之间的满足二次函数关系,其具体对应值如下表所示:
地铁站 | A | B | C | D | E |
X(千米) | 3 |
| 4 |
| 5 |
Y2(分钟) | 11 |
| 6 |
| 3 |
(1)求y2关于x的函数表达式;
(2)求小明从学校回到家的时间y(单位:分钟)与x的函数表达式;
(3)请通过计算说明:小明应选择在哪一站下公交车,才能使他从学校回家所需的时间最短?并求出最短时间.