题目内容
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H.点G在⊙O上,过点G作直线EF,交CD延长线于点E,交AB的延长线于点F.连接AG交CD于K,且KE=GE.

(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)若AC∥EF,![]() ,FB=1,求⊙O的半径.
,FB=1,求⊙O的半径.
【答案】(1)相切,理由见解析;(2)4.
【解析】
试题分析:(1)求出∠OGA=∠OAG,∠AKH+∠OAG=90°,∠KGE=∠GKE=∠AKH,推出∠KGE+∠OGA=∠AKH+∠OAG=90°,得出∠OGE=90°,根据切线的判定推出即可;
(2)求出∠F=∠CAH,∠OGF=∠CHA=90°,推出Rt△AHC∽Rt△FGO,得出![]() ,根据
,根据![]()
求出![]() ,得出方程
,得出方程![]() ,解出即可.
,解出即可.
试题解析:(1)如图,连接OG.
∵OA=OG,∴∠OGA=∠OAG.
∵CD⊥AB,∴∠AKH+∠OAG=90°.
∵KE=GE,
∴∠KGE=∠GKE=∠AKH.
∴∠KGE+∠OGA=∠AKH+∠OAG=90°.
∴∠OGE=90°,即OG⊥EF.
又∵G在圆O上,∴EF与圆O相切.
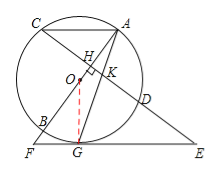
(2)∵AC∥EF, ∴∠F=∠CAH,
∴Rt△AHC∽ Rt△FGO. ∴![]() .
.
∵在Rt△OAH中,![]() ,设AH=3t,则AC=5t,CH=4t.
,设AH=3t,则AC=5t,CH=4t.
∴![]() . ∴
. ∴![]() .
.
∵FB=1 ∴![]() ,解得:OG=4.
,解得:OG=4.
∴圆O的半径为4 .

练习册系列答案
相关题目