题目内容
如图,在以O为圆心的两个同心圆中,大圆的弦AB是小圆的切线,P为切点,设AB=12,则两圆构成圆环面积为______.


连接OA、OB、OP,
∵大圆的弦AB是小圆的切线,
∴OP⊥AB,AP=PB,
∴OB2-OP2=(12÷2)2=36,
∵S圆环=S大-S小=π•OB2-π•OP2=π•(OB2-OP2),
∴S圆环=36π.
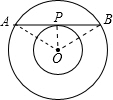
∵大圆的弦AB是小圆的切线,
∴OP⊥AB,AP=PB,
∴OB2-OP2=(12÷2)2=36,
∵S圆环=S大-S小=π•OB2-π•OP2=π•(OB2-OP2),
∴S圆环=36π.


练习册系列答案
相关题目