题目内容
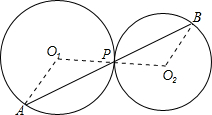
如图,已知扇形AOB,OA⊥OB,C为OB上一点,以OA为直线的半圆O1与以BC为直径的半圆O2相切于点D.
(1)若⊙O1的半径为R,⊙O2的半径为r,求R与r的比;
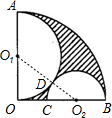
(2)若扇形的半径为12,求图中阴影部分面积.

(1)若⊙O1的半径为R,⊙O2的半径为r,求R与r的比;
(2)若扇形的半径为12,求图中阴影部分面积.

(1)连接O1O2,
∴O1O2=R+r,OO2=2R-r,OO1=R,在Rt△OO1O2中,由勾股定理,得
(R+r)2=R2+(2R-r)2
6r=4R,
∴
=
;
(2)∵2R=12,
∴R=6,
∴
=
,
∴r=4,
S阴影=
π×144-
π×36-
π×16,
=36π-18π-8π
=10π.
∴O1O2=R+r,OO2=2R-r,OO1=R,在Rt△OO1O2中,由勾股定理,得
(R+r)2=R2+(2R-r)2
6r=4R,
∴
| R |
| r |
| 3 |
| 2 |
(2)∵2R=12,
∴R=6,
∴
| 6 |
| r |
| 3 |
| 2 |
∴r=4,
S阴影=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
=36π-18π-8π
=10π.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目



 半圆,EF是这两个半圆的外公切线,E、F为切点.
半圆,EF是这两个半圆的外公切线,E、F为切点.