题目内容
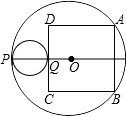
如图,PQ=10,以PQ为直径的圆与一个以20为半径的⊙O内切于点P,与正方形ABCD切于点Q,其中A、B两点在⊙O上.若AB=m+
,其中m、n是整数,求m+n的值.
| n |

连接OA,
∵两圆内切,
∴P、Q、O共线,设过P、Q、O的直线交AB于R,AB=x,
则OQ=OP-PQ=10,RO=RQ-OQ=x-10,(2分)
∵CD与小圆切于点Q,
∴QR⊥CD,QR⊥AB,
∴根据垂径定理知AR=
AB=
x,(4分)
∴在Rt△OAR中,OA2=OR2+AR2,
即(10-x)2+(
)2=202,(6分)
解得:x=8±
,(8分)
而AB=m+
,m、n为整数,
∴m=8,n=304,
∴m+n=312.(10分)
故答案为:312.

∵两圆内切,
∴P、Q、O共线,设过P、Q、O的直线交AB于R,AB=x,
则OQ=OP-PQ=10,RO=RQ-OQ=x-10,(2分)
∵CD与小圆切于点Q,
∴QR⊥CD,QR⊥AB,
∴根据垂径定理知AR=
| 1 |
| 2 |
| 1 |
| 2 |
∴在Rt△OAR中,OA2=OR2+AR2,
即(10-x)2+(
| x |
| 2 |
解得:x=8±
| 304 |
而AB=m+
| n |
∴m=8,n=304,
∴m+n=312.(10分)
故答案为:312.


练习册系列答案
相关题目