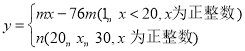Question

【题目】对于实数，若存在坐标同时满足一次函数和反比例函数，则二次函数为一次函数和反比例函数的“共享”函数．

（1）试判断（需要写出判断过程）：一次函数和反比例函数是否存在“共享”函数？若存在，写出它们的“共享”函数和实数对坐标；

（2）已知整数满足条件：，并且一次函数与反比例函数存在“共享”函数，求整数的值．

Answer 1

【答案】（1）存在，二次函数为一次函数和反比例函数的“共享”函数，实数对坐标为和；（2）．

【解析】

（1）联立方程即可求出实数对坐标，然后根据“共享”函数的定义即可求出结论；

（2）根据“共享”函数的定义即可列出关于m、n、t的关系式，然后根据不等关系式即可求出结论．

解：（1）存在，

令，

解得或

∴存在和同时满足和，其中p=-1，q=4，k=3

∴二次函数为一次函数和反比例函数的“共享”函数

实数对坐标为和．

（2）与的“共享”函数是，

由题意，得

与的“共享”函数为，

，即，

又，

，

解得：1＜m＜3

∵为整数，

．