Question

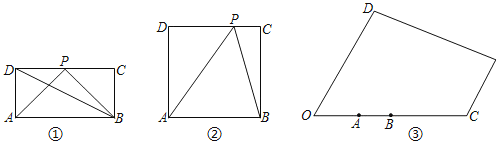
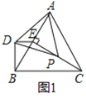
【题目】如图1，在等边和等边中，，点P在的高上（点与点不重合），点在点的左侧，连接，.

（1）求证：；

（2）当点与点重合时，延长交于点，请你在图2中作出图形，并求出的长；

（3）直接写出线段长度的最小值.

Answer 1

【答案】（1）见解析；（2）作图见解析，； （3） .

【解析】

(1)利用条件证明,即可证明BD=CP;

(2)根据等边三角形的性质,求出∠BCE=30°,再利用三角函数解出BF即可.

(3) 取的中点，连接，证明，长度的最小值就是DE长的最小值，过点作于，求出PF即可.

（1）证明：是等边三角形，

∴，，

∵是等边三角形，

∴，，

∴，

∴，

∴，

∴；

（2）解：如图2，

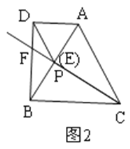
∵是等边三角形，

∴当点与点重合时，有，，

∵，

∴，，

∴，

∴，

在中，

∵，，

∴；

（3）长度的最小值是，

理由是：如图3，由（1）知：，

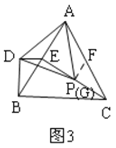
∴取的中点，连接，则，

∴长度的最小值就是DE长的最小值，

过点作于，垂足就是最小时点的位置，此时，故长度的最小值是.