题目内容
【题目】关于x的方程2x2﹣5xsinA+2=0有两个相等的实数根,其中∠A是锐角三角形ABC的一个内角.
(1)求sinA的值;
(2)若关于y的方程y2﹣10y+k2﹣4k+29=0的两个根恰好是△ABC的两边长,求△ABC的周长.
【答案】(1)sinA=![]() ;(2)△ABC的周长为
;(2)△ABC的周长为![]() 或16.
或16.
【解析】
(1)利用判别式的意义得到△=25sin2A-16=0,解得sinA=![]() ;
;
(2)利用判别式的意义得到100-4(k2-4k+29)≥0,则-(k-2)2≥0,所以k=2,把k=2代入方程后解方程得到y1=y2=5,则△ABC是等腰三角形,且腰长为5.
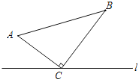
分两种情况:当∠A是顶角时:如图,过点B作BD⊥AC于点D,利用三角形函数求出AD=3,BD=4,再利用勾股定理求出BC即得到△ABC的周长;
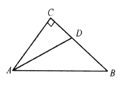
当∠A是底角时:如图,过点B作BD⊥AC于点D,在Rt△ABD中,AB=5,利用三角函数求出AD得到AC的长,从而得到△ABC的周长.
(1)根据题意得△=25sin2A-16=0,
∴sin2A=![]() ,
,
∴sinA=±![]() ,
,
∵∠A为锐角,
∴sinA=![]() ;
;
(2)由题意知,方程y2-10y+k2-4k+29=0有两个实数根,
则△≥0,
∴100-4(k2-4k+29)≥0,
∴-(k-2)2≥0,
∴(k-2)2≤0,
又∵(k-2)2≥0,
∴k=2,
把k=2代入方程,得y2-10y+25=0,
解得y1=y2=5,∴△ABC是等腰三角形,且腰长为5.
分两种情况:
当∠A是顶角时:如图,过点B作BD⊥AC于点D,在Rt△ABD中,AB=AC=5,
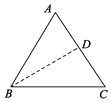
∵sinA=![]() ,
,
∴AD=3,BD=4∴DC=2,
∴BC=2![]() .
.
∴△ABC的周长为10+2![]() ;
;
当∠A是底角时:如图,过点B作BD⊥AC于点D,
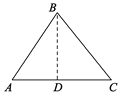
在Rt△ABD中,AB=5,
∵sinA=![]() ,
,
∴AD=DC=3,
∴AC=6.
∴△ABC的周长为16,
综合以上讨论可知:△ABC的周长为10+2![]() 或16.
或16.

 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案