ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΆΦ1 «Ρ≥‘Γ “Μ®»ς ΒΨΑΆΦΘ§ΆΦ2 «ΗΟΜ®»ςΒΡ≤ύΟφ Ψ“βΆΦΘ°“―÷ΣΜνΕ·ΒςΫΎΒψBΩ…“‘…œœ¬Βς’ϊΗΏΕ»Θ§άκΒΊΟφCDΒΡΨύάκBCΘΫ160cmΘ°…ηΜ®»ς±έ”κ«ΫΟφΒΡΦ–Ϋ«ΈΣΠΝΘ§Ω…“‘≈ΛΕ·Μ®»ς±έΒς’ϊΫ«Ε»Θ§«“Μ®»ς±έ≥ΛABΘΫ30cmΘ°ΦΌ…ηΥ°÷υAE¥Ι÷±AB÷±œΏ≈γ…δΘ§–ΓΜΣ‘Ύάκ«ΫΟφΨύάκCDΘΫ120cm¥ΠΝή‘ΓΘ°

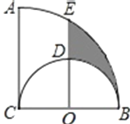
Θ®1Θ©Β±ΠΝΘΫ30Γψ ±Θ§Υ°÷υ’ΐΚΟ¬δ‘Ύ–ΓΜΣΒΡΆΖΕΞ…œΘ§«σ–ΓΜΣΒΡ…μΗΏDEΘ°
Θ®2Θ©»γΙϊ–ΓΜΣ“Σœ¥Ϋ≈Θ§–η“ΣΒς’ϊΥ°÷υAEΘ§ ΙΒψE”κΒψD÷ΊΚœΘ§Βς’ϊΒΡΖΫ Ϋ”–ΝΫ÷÷ΘΚ
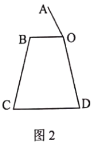
ΔΌΤδΥϊΧθΦΰ≤Μ±δΘ§÷Μ“ΣΑ―ΜνΕ·ΒςΫΎΒψBœρœ¬“ΤΕ·Φ¥Ω…Θ§“ΤΕ·ΒΡΨύάκBF”κ–ΓΜΣΒΡ…μΗΏDE”– ≤Ο¥ ΐΝΩΙΊœΒΘΩ÷±Ϋ”–¥≥ωΡψΒΡΫα¬έΘΜ
ΔΎΜνΕ·ΒςΫΎΒψB≤ΜΕ·Θ§÷Μ“ΣΒς’ϊΠΝΒΡ¥σ–ΓΘ§‘ΎΆΦ3÷–Θ§ ‘«σΠΝΒΡΕ» ΐΘ°
Θ®≤ΈΩΦ ΐΨίΘΚ![]() Γ÷1.73Θ§sin8.6ΓψΓ÷0.15Θ§sin36.9ΓψΓ÷0.60Θ§tan36.9ΓψΓ÷0.75Θ©
Γ÷1.73Θ§sin8.6ΓψΓ÷0.15Θ§sin36.9ΓψΓ÷0.60Θ§tan36.9ΓψΓ÷0.75Θ©
ΓΨ¥πΑΗΓΩΘ®1Θ©125.4cmΘΜΘ®2Θ©ΔΌBFΘΫDEΘΜΔΎ61.7ΓψΘ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΙΐΒψAΉςAGΓΆCBΒΡ―”≥ΛœΏ”ΎΒψGΘ§ΫΜDEΒΡ―”≥ΛœΏ”ΎΒψHΘ§άϊ”ΟΚ§30Ε»Ϋ«ΒΡ÷±Ϋ«»ΐΫ«–ΈΒΡ–‘÷ Φ¥Ω…«σ≥ω¥πΑΗΘ°
Θ®2Θ©ΔΌ”…ΤΫ––ΥΡ±Ώ–ΈΒΡ≈–Ε®”κ–‘÷ Φ¥Ω…÷ΣΒάBFΘΫDEΘΜ
ΔΎ”…Ι¥Ι…Ε®άμΩ…«σ≥ωBDΒΡ≥ΛΕ»Θ§»ΜΚσΗυΨί»ώΫ«»ΐΫ«Κ· ΐΒΡΕ®“εΩ…«σ≥ωΓœ1”κΓœ2ΒΡΕ» ΐΘ§¥”ΕχΩ…«σ≥ωΠΝΒΡΕ» ΐΘ°
ΫβΘΚΘ®1Θ©»γΆΦΘ§ΙΐΒψAΉςAGΓΆCBΒΡ―”≥ΛœΏ”ΎΒψGΘ§ΫΜDEΒΡ―”≥ΛœΏ”ΎΒψHΘ§
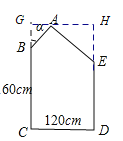
ΓΏΓœCΘΫΓœDΘΫ90ΓψΘ§
ΓύΥΡ±Ώ–ΈGCDHΈΣΨΊ–ΈΘ§
ΓύGHΘΫCDΘΫ120Θ§DHΘΫCGΘ§ΓœHΘΫ90ΓψΘ§
‘ΎRtΓςABG÷–Θ§
ΓœABGΘΫΠΝΘΫ30ΓψΘ§ABΘΫ30Θ§
ΓύAGΘΫ15Θ§
ΓύAHΘΫ120©¹15ΘΫ105Θ§
ÿAEâABȧ
ΓύΓœEAHΘΫ30ΓψΘ§
”÷ΓΏΓœHΘΫ90ΓψΘ§
ΓύEHΘΫAH![]() tan30ΓψΘΫ35
tan30ΓψΘΫ35![]() Θ§
Θ§
ΓύEDΘΫHD©¹HEΘΫ160+15![]() ©¹35
©¹35![]() Γ÷125.4Θ®cmΘ©
Γ÷125.4Θ®cmΘ©
Θ®2Θ©ΔΌBFΘΫDEΘΜ
ΔΎ»γΆΦΘ§Ν§Ϋ”BD
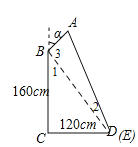
‘ΎRtΓςBCD÷–Θ§
BDΘΫ![]() ΘΫ200Θ§
ΘΫ200Θ§
ΓύsinΓœ1ΘΫ![]() ΘΫ0.6Θ§
ΘΫ0.6Θ§
ΓύΓœ1Γ÷36.9ΓψΘ§
‘ΎRtΓςBAD÷–Θ§ABΘΫ30Θ°
ΓύsinΓœ2ΘΫ![]() ΘΫ
ΘΫ![]() ΘΫ0.15Θ§
ΘΫ0.15Θ§
ΓύΓœ2Γ÷8.6ΓψΘ§
ΓύΓœ3Γ÷90Γψ©¹8.6ΓψΘΫ81.4ΓψΘ§
ΓύΠΝΘΫ180Γψ©¹Γœ1©¹Γœ3Γ÷180Γψ©¹36.9Γψ©¹81.4ΓψΘΫ61.7ΓψΘ°

 Οϊ≈Τ―ß–ΘΖ÷≤ψ÷ή÷ή≤βœΒΝ–¥πΑΗ
Οϊ≈Τ―ß–ΘΖ÷≤ψ÷ή÷ή≤βœΒΝ–¥πΑΗ ΜΤΗ‘ΚΘΒμ»Ϊ≥Χ≈ύ”≈≤β ‘ΨμœΒΝ–¥πΑΗ
ΜΤΗ‘ΚΘΒμ»Ϊ≥Χ≈ύ”≈≤β ‘ΨμœΒΝ–¥πΑΗ