Question

【题目】如图，一块余料ABCD，AD∥BC，现进行如下操作：以点B为圆心，适当长为半径画弧，分别交BA，BC于点G，H；再分别以点G，H为圆心，大于GH的长为半径画弧，两弧在∠ABC内部相交于点O，画射线BO，交AD于点E．

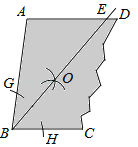
（1）求证：AB=AE；

（2）若∠A=100°，求∠EBC的度数．

Answer 1

【答案】（1）证明见试题解析；（2）40°．

【解析】试题分析：（1）由角平分线的性质，可以得到∠AEB=∠EBC，由角平分线的性质，得到∠EBC=∠ABE，由等腰三角形的判定，可得答案；

（2）由三角形的内角和定理，可得∠AEB，由平行线的性质，可得答案．

试题解析：（1）∵AD∥BC，∴∠AEB=∠EBC，∵ BE是∠ABC的角平分线，∴∠EBC=∠ABE，∴∠AEB=∠ABE，∴AB=AE；

（2）∵∠A=100°，∠ABE=∠AEB，∴∠ABE=∠AEB=40°，∵AD∥BC，∴∠EBC=∠AEB=40°．