题目内容
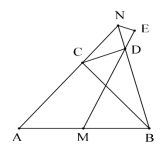
【题目】已知平行四边形ABCD中,N是边BC上一点,延长DN、AB交于点Q,过A作AM⊥DN于点M,连接AN,则AD⊥AN.
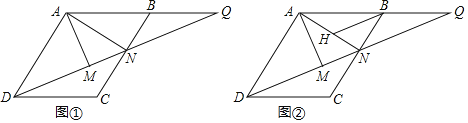
(1)如图①,若tan∠ADM=![]() ,MN=3,求BC的长;
,MN=3,求BC的长;
(2)如图②,过点B作BH∥DQ交AN于点H,若AM=CN,求证:DM=BH+NH.
【答案】(1)BC=![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)如图①中,设AM=3k,DM=4k,则AD=5k,由△ADM∽△NDA,可得AD2=DMAN,由此构建方程即可解决问题.
(2)如图②中,连接CH,在DM上取一点K,使得DK=BH.证明△ADK≌△CBH(SAS),推出AK=CH,再证明Rt△AMK≌Rt△CNH(HL),推出MK=HN即可解决问题.
(1)解:如图①中,
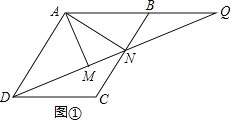
∵AM⊥DN,
∴∠AMD=90°,
∵tan∠ADM=![]() =
=![]() ,
,
∴可以假设AM=3k,DM=4k,则AD=5k,
∵AD⊥AN,
∴∠DAN=90°=∠AMD,
∵∠ADM=∠ADN,
∴△ADM∽△NDA,
∴AD2=DMAN,
∴(5k)2=4k(4k+3),
解得k=![]() ,
,
∴AD=![]() ,
,
∵四边形ABCD是平行四边形,
∴BC=AD=![]() .
.
(2)证明:如图②中,连接CH,在DM上取一点K,使得DK=BH.
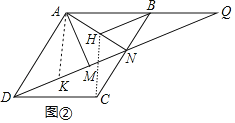
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠ADK=∠BNQ,
∵BH∥DQ,
∴∠CBH=∠BNQ,
∴∠ADK=∠CBH,
∵DK=BH,DA=BC,
∴△ADK≌△CBH(SAS),
∴AK=CH,
∵AM⊥DQ,AN⊥AD,AD∥BC,
∴AN⊥BC,
∴∠AMK=∠CNH=90°,
∵AM=CN,
∴Rt△AMK≌Rt△CNH(HL),
∴MK=NH,
∴DM=DK+MK=BH+HN.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目