Question

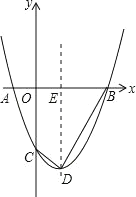
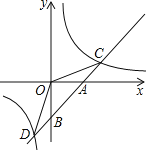
【题目】如图，直线y＝kx+b与x轴交于点A，与y轴交于点B，OB＝4，sin∠CBO＝．

（1）求直线AB的解析式；

（2）直线AB与反比例函数y＝相交于C、D两点（C点在第一象限），求S△DOC的面积．

Answer 1

【答案】（1）直线AB的解析式为y＝x﹣4；（2）S△DOC的面积：16.

【解析】

（1）由sin∠CBO＝得出∠CBO＝45°，即可得出△AOB是等腰直角三角形，从而求得A、B的坐标，然后根据待定系数法即可求得直线AB的解析式；

（2）解析式联立求得交点C、D的坐标，然后根据S△DOC＝S△BOC+S△BOD即可求得．

解：（1）∵OB＝4，sin∠CBO＝．

∴∠CBO＝45°，

∴△AOB是等腰直角三角形，

∴OA＝OB＝4，

∴A（4，0），B（0，﹣4），

代入y＝kx+b得，

解得k＝1，b＝﹣4，

∴直线AB的解析式为y＝x﹣4；

（2）解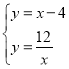

得或，

∴C（6，2），D（﹣2，﹣6），

∴S△DOC＝S△BOC+S△BOD＝＝16．