��Ŀ����
����Ŀ�����壺���ǰ�ƽ������һ������F��һ����ֱ��l��l��������F��������ȵĵ�Ĺ켣���������������е�����ɵ�ͼ�Σ����������ߣ���F���������ߵĽ��㣬ֱ��l���������ߵ��ߣ�
��1����֪�����ߵĽ���F��0�� ![]() ������l��
������l�� ![]() ���������ߵĽ���ʽ��
���������ߵĽ���ʽ��
��2����֪�����ߵĽ���ʽΪ��y=x2��n2 �� ��A��0�� ![]() ����n��0����B��1��2��n2����PΪ��������һ�㣬��PA+PB����Сֵ����ʱP�����ꣻ
����n��0����B��1��2��n2����PΪ��������һ�㣬��PA+PB����Сֵ����ʱP�����ꣻ
��3������2���������ߵĶ���ΪC����������x�����������ֱ���D��E����C��D��E��������M����M���Ƿ���ڶ���N�������ڣ����N�����겢ָ�������Ķ���N�м������������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺������������һ�㣨x��y����
�ɶ���֪��x2+��y�� ![]() ��2=|y+
��2=|y+ ![]() |2��
|2��
���y=ax2��
��2��
�⣺��ͼ1���ɣ�1����������y=x2�Ľ���Ϊ��0�� ![]() ������Ϊy=��
������Ϊy=�� ![]() ��
��
��y=x2��n2��y=x2����ƽ��n2����λ���ã�
���佹��ΪA��0�� ![]() ��n2������Ϊy=��
��n2������Ϊy=�� ![]() ��n2��
��n2��
�ɶ���֪PΪ�������ϵĵ㣬��PA=PH��
��PA+PH���ΪP��B��A���ߣ���ʱP��P�䴦��
��x=1��
��y=1��n2��2��n2��
���B���������ڣ�
��BI=yB��yI=2��n2������ ![]() ��n2��=
��n2��= ![]() ��
��
��PA+PB����СֵΪ ![]() ����ʱP������Ϊ��1��1��n2����
����ʱP������Ϊ��1��1��n2����
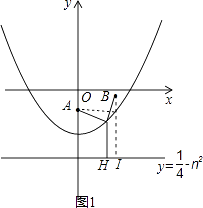
��3��
�⣺�ɣ�2��֪E��|n|��0����C��0��n2����
��OQ=m��m��0������CQ=QE=n2��m��
��Rt��OQE�У��ɹ��ɶ�����|n|2+m2=��n2��m��2��
���m= ![]() ��
�� ![]() ��
��
��QC= ![]() +
+ ![]() =QN��
=QN��
��ON=QN��m=1��
����N��0��1����
��AM������N��0��1����
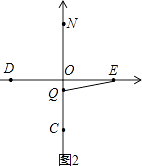
����������1��ֱ�Ӹ����¶��弴����������ߵĽ���ʽ����2��������������ߵĽ��������Լ��߷��̣�����PA+PH���ʱ��P��B��A���ߣ��ݴ����PA+PB����Сֵ����ʱP�����ꣻ��3����OQ=m��m��0������CQ=QE=n2��m����Rt��OQE�У��ɹ��ɶ�����|n|2+m2=��n2��m��2 �� �������ON�Ƕ�ֵ���ݴ������жϣ�
�����㾫�������ڱ��⿼��Ķ��κ�����ͼ��Ͷ��κ��������ʣ���Ҫ�˽���κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С���ܵó���ȷ�𰸣�

 ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�