题目内容
【题目】如图1，平面直角坐标系中，等腰直角三角形的直角边BC在x轴正半轴上滑动，点C的坐标为（t，0），直角边AC=4，经过O，C两点做抛物线y1=ax（x﹣t）（a为常数，a＞0），该抛物线与斜边AB交于点E，直线OA：y2=kx（k为常数，k＞0）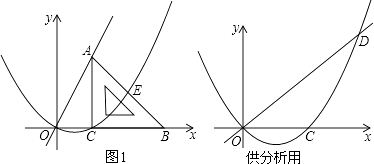
（1）填空：用含t的代数式表示点A的坐标及k的值：A ， k=；
（2）随着三角板的滑动，当a= 
时：
①请你验证：抛物线y1=ax（x﹣t）的顶点在函数y= 
的图象上；
②当三角板滑至点E为AB的中点时，求t的值；
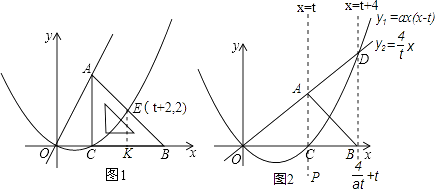
（3）直线OA与抛物线的另一个交点为点D，当t≤x≤t+4，|y2﹣y1|的值随x的增大而减小，当x≥t+4时，|y2﹣y1|的值随x的增大而增大，求a与t的关系式及t的取值范围．
【答案】
（1）（t，4）；
（k＞0）
（2）
解：①当a= 
时，y1= x（x﹣t），其顶点坐标为（ 
，﹣ 
）．
对于y= 
来说，当x= 时，y=- × 
=﹣ ，即点（ ，﹣ ）在抛物线y= 上．
故当a= 时，抛物线y1=ax（x﹣t）的顶点在函数y= 的图象上；
②如图1，过点E作EK⊥x轴于点K．
∵AC⊥x轴，
∴AC∥EK．
∵点E是线段AB的中点，
∴K为BC的中点，
∴EK是△ACB的中位线，
∴EK= 
AC=2，CK= BC=2，
∴E（t+2，2）．
∵点E在抛物线y1= x（x﹣t）上，
∴ （t+2）（t+2﹣t）=2，
解得t=2．
（3）
解：如图2，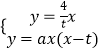 
，则 x=ax（x﹣t），
解得x= 
+t，或x=0（不合题意，舍去）．
故点D的横坐标是 +t．
当x= +t时，|y2﹣y1|=0，由题意得t+4= +t，
∴at=1．
∵y2﹣y1= x﹣ax（x﹣t）=﹣ax2+（at+ ）x=﹣a[x2﹣（t+ ）x+（ + 
）2]+a（ + ）2
=﹣a[x﹣（ + ）]2+a（ + ）2
∴当x= + 时，y2﹣y1取得最大值，
又∵当x= +t时，|y2﹣y1|=0，
∴当 + ≤x≤ +t时，|y2﹣y1|随x的增大而减小；当x≥ +t时，|y2﹣y1|随x的增大而增大．
根据题意需要满足当t≤x≤t+4，|y2﹣y1|的值随x的增大而减小，当x≥t+4时，|y2﹣y1|的值随x的增大而增大，
∴t≥ + 可满足条件，
∵at=1，
∴解得t≥4．
综上所述，a与t的关系式及t的取值范围为at=1（t≥4）．
【解析】 解：（1）∵点C的坐标为（t，0），直角边AC=4，∴点A的坐标是（t，4）．又∵直线OA：y2=kx（k为常数，k＞0），∴4=kt，则k= （k＞0）．
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点，需要掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小才能正确解答此题．
