题目内容
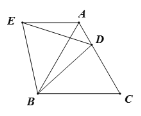
【题目】如图,![]() 中,
中,![]() ,以
,以![]() 为边在
为边在![]() 外作等边三角形
外作等边三角形![]() ,过点
,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,与
,与![]() 相交于点
相交于点![]() ,连接
,连接![]() .
.

(1)说明:![]() ;
;
(2)若![]() ,
,![]() ,
,![]() 是直线
是直线![]() 上的一点.则当
上的一点.则当![]() 在何处时,
在何处时,![]() 最小,并求此时
最小,并求此时![]() 的值.
的值.
【答案】(1)证明见解析;(2)点P在点E处时PB+PC最小,最小值为12cm.
【解析】
(1)根据等边三角形“三合一”的性质证得DE垂直平分AC;然后由垂直平分线的性质可得AE=CE,根据等边对等角、直角三角形的两个锐角互余的性质以及等量代换求得∠BCE=∠B;最后根据等角对等边证得CE=BE,可得AE=CE=BE;(2)由DA⊥AB可得∠BAC=30°,可求出AB的长,由(1)知,DE垂直平分AC,故PC=PA;由等量代换知PB+PC=PB+PA;根据两点之间线段最短可知,当点P、B、A在同一直线上最小,所以点P在E处时最小.
∵DF⊥AC,△ACD是等边三角形,
∴DF垂直平分AC,
∴AE=CE,
∴∠ACE=∠CAE,
∵∠ACB=90°,
∴∠ACE+∠BCE=∠CAE+∠B=90°,
∴∠BCE=∠B,
∴CE=BE,
∴AE=CE=BE;
(2)∵DA⊥AB,∠DAC=60°,
∴∠BAC=30°,
∵∠ACB=90°,BC=6,
∴AB=2BC=12,
由(1)知,DE垂直平分AC,
∴PC=PA,
∴PB+PC=PB+PA;
∴当PB+PC最小时,即PB+PA最小,
∵点P、B、A在同一直线上时,PB+PA最小,
∴点P在点E处时PB+PA最小.即PB+PC最小,
当点P在E处时,PB+PC=BE+CE=BE+AE=AB=12cm.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目