题目内容
【题目】如图,在Rt△ABC中,∠C=90°,把△ABC绕AC边的中点M旋转后得△DEF,若直角顶点F恰好落在AB边上,且DE边交AB边于点G,若AC=4,BC=3,则AG的长为( )

A.![]() B.
B.![]() C.
C.![]() D.1
D.1
【答案】A
【解析】
连接CF,先证明△ACF为直角三角形,再由△ABC中等面积法求出CF,进而求出AF;再证明△DEF为直角三角形,且G为DE的中点,最后AG=AF-GF即可求解.
解:连接CF,如下图所示:
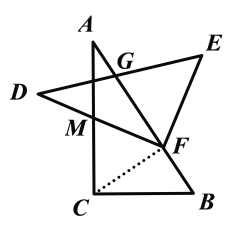
∵M是AC的中点,∴MC=MA
∵M是旋转中心,C绕M点旋转后的落点为F
∴MC=MF
∴∠MCF=∠MFC,
∴MA=MC=MF
∴∠MFA=∠A
在△ACF中,由内角和定理知:∠A +∠MFA+∠ACF+∠CFM=180°
故2∠AFM+2∠CFM=180°
∴∠AFC=90°
∴△ACF为直角三角形,CF⊥AB
由△ABC等面积法知:![]() ,且AB=5
,且AB=5
代入数据解得CF=![]()
∴![]()
∵∠A+∠B=90°,∠A+∠ACF=90°
∴∠ACF=∠B![]()
又DF⊥EF,
∴∠AFD+∠AFE=90°
∵∠AFD+∠MFC=90°
∴∠AFE=∠MFC=∠ACF![]()
由![]() 知:∠B=∠AFE
知:∠B=∠AFE
又由旋转知:∠B=∠E
∴∠AFE=∠E,即GF=GE
由旋转知:∠A=∠D
又∠A=∠AFM
∴∠D=∠AFM,
∴GF=GD
故GF=GE= GD
∴G为Rt△DEF斜边DE上的中点
∴![]()
∴![]()
故答案为:A.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目