Question

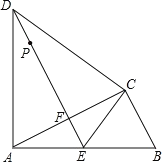
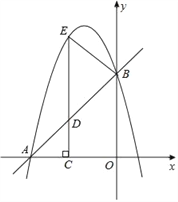
【题目】如图，在平面直角坐标系xOy中，直线y=x+4与坐标轴分别交于A、B两点，抛物线y=﹣x2+bx+c过A、B两点，点D为线段AB上一动点，过点D作CD⊥x轴于点C，交抛物线于点E．

（1）求抛物线的解析式．

（2）求△ABE面积的最大值．

（3）连接BE，是否存在点D，使得△DBE和△DAC相似？若存在，求出点D坐标；若不存在，说明理由．

Answer 1

【答案】（1）y=﹣x2﹣3x+4．（2）△ABE面积的最大值为8．（3）存在点D，使得△DBE和△DAC相似，点D的坐标为（﹣3，1）或（﹣2，2）．

【解析】试题分析：（1）首先求出点A、B的坐标，然后利用待定系数法求出抛物线的解析式；

（2）设点C坐标为（m，0）（m＜0），则点E坐标为（m，-m2-3m+4），从而得出OC=-m、OF=-m2-3m+4、BF=-m2-3m，根据S△ABE=S梯形AOFE-S△AOB-S△BEF得出S=-2（m+2）2+8，据此可得答案；

（3）由于△ACD为等腰直角三角形，而△DBE和△DAC相似，则△DBE必为等腰直角三角形．分两种情况讨论，要点是求出点E的坐标，由于点E在抛物线上，则可以由此列出方程求出未知数．

试题解析：（1）在直线解析式y=x+4中，令x=0，得y=4；令y=0，得x=﹣4，

∴A（﹣4，0），B（0，4）．

∵点A（﹣4，0），B（0，4）在抛物线y=﹣x2+bx+c上，

∴，

解得：b=﹣3，c=4，

∴抛物线的解析式为：y=﹣x2﹣3x+4．

（2）如图，连接AE、过点E作EF⊥y轴于点F，

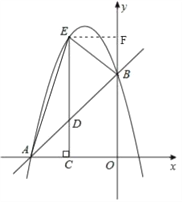
设点C坐标为（m，0）（m＜0），则点E坐标为（m，﹣m2﹣3m+4），

则OC=﹣m，OF=﹣m2﹣3m+4，

∵OA=OB=4，

∴BF=﹣m2﹣3m，

则S△ABE=S梯形AOFE﹣S△AOB﹣S△BEF

=×（﹣m+4）（﹣m2﹣3m+4）﹣×4×4﹣×（﹣m）×（﹣m2﹣3m）．

=﹣2m2﹣8m

=﹣2（m+2）2+8，

∵﹣4＜m＜0，

∴当m=﹣2时，S取得最大值，最大值为8．

即△ABE面积的最大值为8．

（3）设点C坐标为（m，0）（m＜0），则OC=﹣m，CD=AC=4+m，BD=OC=﹣m，

则D（m，4+m）．

∵△ACD为等腰直角三角形，△DBE和△DAC相似

∴△DBE必为等腰直角三角形．

i）若∠BED=90°，则BE=DE，

∵BE=OC=﹣m，

∴DE=BE=﹣m，

∴CE=4+m﹣m=4，

∴E（m，4）．

∵点E在抛物线y=﹣x2﹣3x+4上，

∴4=﹣m2﹣3m+4，解得m=0（不合题意，舍去）或m=﹣3，

∴D（﹣3，1）；

ii）若∠EBD=90°，则BE=BD=﹣m，

在等腰直角三角形EBD中，DE=BD=﹣2m，

∴CE=4+m﹣2m=4﹣m，

∴E（m，4﹣m）．

∵点E在抛物线y=﹣x2﹣3x+4上，

∴4﹣m=﹣m2﹣3m+4，解得m=0（不合题意，舍去）或m=﹣2，

∴D（﹣2，2）．

综上所述，存在点D，使得△DBE和△DAC相似，点D的坐标为（﹣3，1）或（﹣2，2）．