题目内容
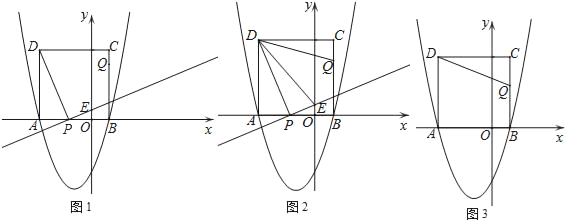
【题目】如图,在菱形![]() 中
中![]() ,E为对角线
,E为对角线![]() 上一点,F是
上一点,F是![]() 延长线上一点,连接
延长线上一点,连接![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求证:![]() ;
;
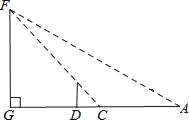
(2)若点G为![]() 的中点,连接
的中点,连接![]() ,求证:
,求证:![]() .
.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)根据菱形的性质,得到AD=CD,∠ABC=∠ADC=∠ACD=∠CAD=60°,然后根据等式的性质求得∠ADE=∠CDF,从而利用ASA定理判定三角形全等,问题得解;
(2)过点B作BH∥AC,交AG的延长线于点H,根据菱形的性质结合(1)中的结论判定△ABE≌△ADE≌△CDF,利用ASA定理判定△BHG≌△EAG,利用SAS定理判定△ABH≌△ACF,从而得到AH=AF,使问题得解.
解:在菱形ABCD中,∵![]()
∴AD=CD,∠ABC=∠ADC=∠ACD=∠CAD=∠ACB=60°
∴∠DCF=60°
又∵![]()
∴∠ADE+∠EDC=∠CDF+∠EDC=60°
∴∠ADE=∠CDF,
在△ADE和△CDF中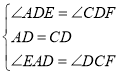
∴△ADE≌△CDF
∴![]() ;
;
(2)过点B作BH∥AC,交AG的延长线于点H
在菱形ABCD中,∠ABE=∠ADE,AB=AD,AE=AE
又由(1)可知△ADE≌△CDF
∴△ABE≌△ADE≌△CDF
∴AE=CF
∵BH∥AC,点G是BE的中点
∴∠H=∠GAE,BG=EG,∠HBG=∠ACB=60°
∴∠ABH=∠ACF=120°
又∵∠AGE=∠HGB
∴△BHG≌△EAG
∴BH=AE=CF,AG=GH
又∵AB=AC
∴△ABH≌△ACF
∴AH=AF=AG+GH=2AG
即![]() .
.

 高中必刷题系列答案
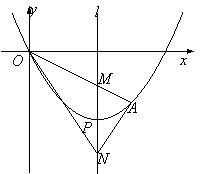
高中必刷题系列答案【题目】如图,平面直角坐标系中直线![]() :
:![]() 分别与x轴,y轴交于点A和点B,过点A的直线
分别与x轴,y轴交于点A和点B,过点A的直线![]() 与y轴交于点C,
与y轴交于点C,![]() .
.

(1)求直线![]() 的解析式;
的解析式;
(2)若D为线段![]() 上一点,E为线段
上一点,E为线段![]() 上一点,当
上一点,当![]() 时,求
时,求![]() 的最小值,并求出此时点E的坐标.
的最小值,并求出此时点E的坐标.
【题目】为了加强对校内外的安全监控,创建平安校园,某学校计划增加![]() 台监控摄像设备,现有甲、乙两种型号的设备,其中每台价格、有效监控半径如表所示,经调查,购买
台监控摄像设备,现有甲、乙两种型号的设备,其中每台价格、有效监控半径如表所示,经调查,购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备少
台乙型设备少![]() 元,购买
元,购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备多
台乙型设备多![]() 元.
元.
甲型 | 乙型 | |
价格(元/台) |
|
|
有效半径(米/台) |
|
|
(![]() )求
)求![]() ,
,![]() 的值;
的值;
(![]() )若购买该批设备的资金不超过
)若购买该批设备的资金不超过![]() 元,且两种型号的设备均要至少买一台,学校有哪几种购买方案?
元,且两种型号的设备均要至少买一台,学校有哪几种购买方案?
(![]() )在(
)在(![]() )的条件下,若要求监控半径覆盖范围不低于
)的条件下,若要求监控半径覆盖范围不低于![]() 米,为了节约资金,请你设计一种最省钱的购买方案.
米,为了节约资金,请你设计一种最省钱的购买方案.