题目内容
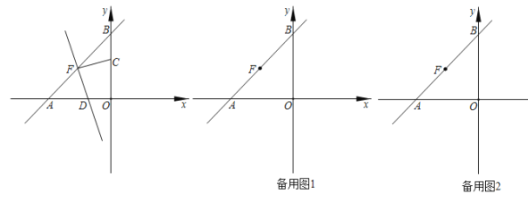
【题目】如图,已知直线![]() 经过点
经过点![]() ,交x轴于点A,y轴于点B,F为线段AB的中点,动点C从原点出发,以每秒1个位长度的速度沿y轴正方向运动,连接FC,过点F作直线FC的垂线交x轴于点D,设点C的运动时间为t秒.
,交x轴于点A,y轴于点B,F为线段AB的中点,动点C从原点出发,以每秒1个位长度的速度沿y轴正方向运动,连接FC,过点F作直线FC的垂线交x轴于点D,设点C的运动时间为t秒.
![]() 当
当![]() 时,求证:
时,求证:![]() ;
;
![]() 连接CD,若
连接CD,若![]() 的面积为S,求出S与t的函数关系式;
的面积为S,求出S与t的函数关系式;
![]() 在运动过程中,直线CF交x轴的负半轴于点G,
在运动过程中,直线CF交x轴的负半轴于点G,![]() 是否为定值?若是,请求出这个定值;若不是,请说明理由.
是否为定值?若是,请求出这个定值;若不是,请说明理由.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)连接OF,根据“直线![]() 经过点
经过点![]() ”可得k=1,进而求出A(﹣4,0),B(0,4),得出△AOB是等腰直角三角形,得出∠CBF=45°,得出OF=
”可得k=1,进而求出A(﹣4,0),B(0,4),得出△AOB是等腰直角三角形,得出∠CBF=45°,得出OF=![]() AB=BF,OF⊥AB,得出∠OFD=∠BFC,证得△BCF≌△ODF,即可得出结论
AB=BF,OF⊥AB,得出∠OFD=∠BFC,证得△BCF≌△ODF,即可得出结论
(2)①根据全等三角形的性质可得出0<t<4时,BC=OD=t﹣4,再根据勾股定理得出CD2=2t2-8t+16,证得△FDC是等腰直角三角形,得出![]() ,即可得出结果;
,即可得出结果;
②同理当t≥4时,得出BC=OD=t﹣4,由勾股定理得出CD2=OD2+OC2=2t2﹣8t+16,证出△FDC是等腰直角三角形,得出FC2![]() CD2,即可得出结果;
CD2,即可得出结果;
(3)由待定系数法求出直线CF的解析式,当y=0时,可得出G![]() ,因此OG
,因此OG![]() ,求出
,求出![]() 即可.
即可.
![]() 证明:连接OF,如图1所示:
证明:连接OF,如图1所示:

![]() 直线
直线![]() 经过点
经过点![]() ,
,
![]() ,解得:
,解得:![]() ,
,
![]() 直线
直线![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,
,
![]() 为线段AB的中点,
为线段AB的中点,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,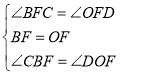 ,
,
![]() ≌
≌![]() ,
,
![]() ;
;
![]() 解:
解:![]() 当
当![]() 时,连接OF,如图2所示:
时,连接OF,如图2所示:
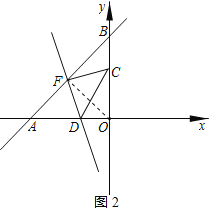
由题意得:![]() ,
,![]() ,
,
由![]() 得:
得:![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,
,
![]() 的面积
的面积![]() ;
;
![]() 当
当![]() 时,连接OF,如图3所示:
时,连接OF,如图3所示:
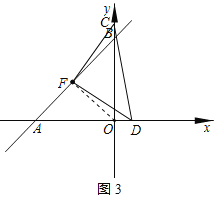
由题意得:![]() ,
,![]() ,
,
由![]() 得:
得:![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,
,
![]() 的面积
的面积![]() ;
;
综上所述,S与t的函数关系式为![]() ;
;
![]() 解:
解:![]() 为定值
为定值![]() ;理由如下:
;理由如下:
![]() 当
当![]() 时,如图4所示:
时,如图4所示:
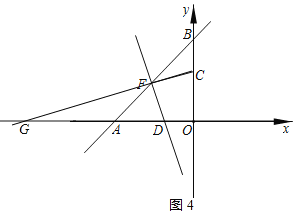
当设直线CF的解析式为![]() ,
,
![]() ,
,![]() ,F为线段AB的中点,
,F为线段AB的中点,
![]() ,
,
把点![]() 代入
代入![]() 得:
得:![]() ,
,
解得:![]() ,
,
![]() 直线CF的解析式为
直线CF的解析式为![]() ,
,
当![]() 时,
时,![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
![]() 当
当![]() 时,如图5所示:
时,如图5所示:
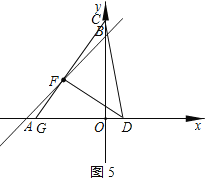
同![]() 得:
得:![]() ;
;
综上所述,![]() 为定值
为定值![]() .
.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案