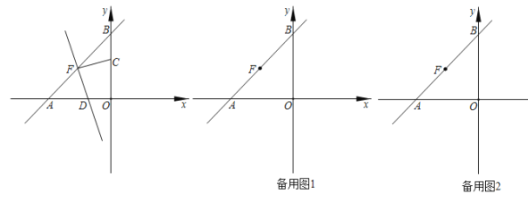
题目内容
【题目】如图，正方形ABCD的边长为1，AC，BD是对角线，将△DCB绕着点D顺时针旋转45°得到△DGH，HG交AB于点E，连接DE交AC于点F，连接FG．则下列结论：
①四边形AEGF是菱形；②△HED的面积是1﹣
；③∠AFG=112.5°；④BC+FG=
．其中正确的结论是（ ）
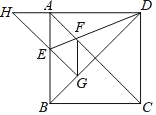
A. ①②③ B. ①②④ C. ①③④ D. ②③④
【答案】B
【解析】
∵四边形ABCD是正方形，
∴AD=DC=BC=AB，∠DAB=∠ADC=∠DCB=∠ABC=90°，∠ADB=∠BDC=∠CAD=∠CAB=45°，
∵△DHG是由△DBC旋转得到，
∴DG=DC=AD，∠DGE=∠DCB=∠DAE=90°，
在Rt△ADE和Rt△GDE中，DE=DE，DA=DG，
∴△AED≌△GED，
∴∠ADE=∠EDG=22.5°，AE=EG，
∴∠AED=∠AFE=67.5°，
∴AE=AF，同理EG=GF，
∴AE=EG=GF=FA，
∴四边形AEGF是菱形，①正确，
∴∠AFG=67.5°×2=135°，③错误．
根据题意可求得BD=
，BG=BD-DG=BD-CD=-1，
在等腰直角三角形EGB中，可求得BE=2-，即可求AE=AB-BE=1-(2-)=-1，
所以AH=AE=-1，即可得△HED的面积是
,②正确；
由（1）的证明过程可得GF=FA，∠CFD=∠CDF=67.5°，所以CD=CF，即可得AC=CF+AF=CD+FG=，④正确．
综上，正确的结论为①②④．
故选B.
【题目】一根弹簧的长度为10厘米，当弹簧受到
千克的拉力时（不超过10），弹簧的长度是
（厘米），测得有关数据如下表所示：
拉力 | 1 | 2 | 3 | 4 | … |
弹簧的长度 |
|
|
|
| … |
（1）写出弹簧长度（厘米）关于拉力（千克）的函数解析式；
（2）如果拉力是10千克，那么弹簧长度是多少厘米？
（3）当拉力是多少时，弹簧长度是14厘米？
