题目内容
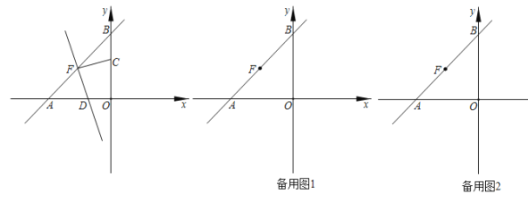
【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连接AC,过![]() 上一点E作EG∥AC交CD的延长线于点G,连接AE交CD于点F,且EG=FG.
上一点E作EG∥AC交CD的延长线于点G,连接AE交CD于点F,且EG=FG.
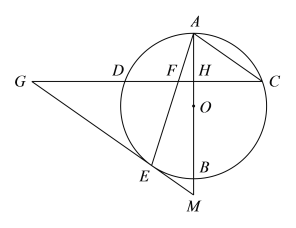
(1)求证:EG是⊙O的切线;
(2)延长AB交GE的延长线于点M,若AH=2,![]() ,求OM的长.
,求OM的长.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)连接OE,如图,通过证明∠GEA+∠OEA=90°得到OE⊥GE,然后根据切线的判定定理得到EG是⊙O的切线;
(2)连接OC,如图,设⊙O的半径为r,则OC=r,OH=r-2,利用勾股定理得到![]() ,解得r=3,然后证明Rt△OEM∽Rt△CHA,再利用相似比计算OM的长.
,解得r=3,然后证明Rt△OEM∽Rt△CHA,再利用相似比计算OM的长.
(1)证明:连接OE,如图,
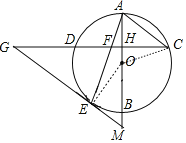
∵GE=GF,
∴∠GEF=∠GFE,
而∠GFE=∠AFH,
∴∠GEF=∠AFH,
∵AB⊥CD,
∴∠OAF+∠AFH=90°,
∴∠GEA+∠OAF=90°,
∵OA=OE,
∴∠OEA=∠OAF,
∴∠GEA+∠OEA=90°,即∠GEO=90°,
∴OE⊥GE,
∴EG是⊙O的切线;
(2)解:连接OC,如图,

设⊙O的半径为r,则OC=r,OH=r-2,
在Rt△OCH中,![]() ,
,
解得r=3,
在Rt△ACH中,AC=![]() ,
,
∵AC∥GE,
∴∠M=∠CAH,
∴Rt△OEM∽Rt△CHA,
∴![]() ,
,
即![]() ,
,
解得:OM=![]() .
.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
【题目】一根弹簧的长度为10厘米,当弹簧受到![]() 千克的拉力时(
千克的拉力时(![]() 不超过10),弹簧的长度是
不超过10),弹簧的长度是![]() (厘米),测得有关数据如下表所示:
(厘米),测得有关数据如下表所示:
拉力 | 1 | 2 | 3 | 4 | … |
弹簧的长度 |
|
|
|
| … |
(1)写出弹簧长度![]() (厘米)关于拉力
(厘米)关于拉力![]() (千克)的函数解析式;
(千克)的函数解析式;
(2)如果拉力是10千克,那么弹簧长度是多少厘米?
(3)当拉力是多少时,弹簧长度是14厘米?