题目内容
【题目】如图,⊙![]() 是
是![]() 的外接圆,
的外接圆,![]() ,
,![]() ,
,![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)若![]() ,
,![]() .求⊙
.求⊙![]() 的半径和线段
的半径和线段![]() 的长.
的长.

【答案】(1)证明见解析;(2)⊙![]() 的半径为4和线段
的半径为4和线段![]() 的长为
的长为![]() .
.
【解析】
(1)连结OA,根据圆周角定理求得∠AOC=90°,又因AD∥OC,根据平行线的性质可得∠AOD=90°,即OA⊥OC,即可证得 AD是⊙O的切线;(2)设⊙O的半径为R,则OA=R,OE=R-2,AE=2![]() ,在Rt△OAE中,根据勾股定理列出方程,解方程求得R的长,即可求得⊙O的半径;延长CO交⊙O于F,连接AF,可得△CEB∽△AEF,根据相似三角形的性质可得
,在Rt△OAE中,根据勾股定理列出方程,解方程求得R的长,即可求得⊙O的半径;延长CO交⊙O于F,连接AF,可得△CEB∽△AEF,根据相似三角形的性质可得![]() ,代入数据求得BE的值即可.
,代入数据求得BE的值即可.
(1)证明:连结OA,如图,
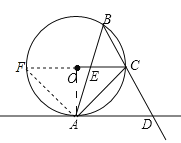
∵∠ABC=45°,
∴∠AOC=2∠ABC=2×45°=90°,
∴AD∥OC,
∴∠AOD=90°,即OA⊥OC,
∴AD是⊙O的切线;
(2)设⊙O的半径为R,则OA=R,OE=R-2,AE=2![]() ,
,
在Rt△OAE中,∵AO2+OE2=AE2,
∴R2+(R-2)2=(2![]() )2,
)2,
解得R=4或R=-2(舍去),
即⊙O的半径为4;
延长CO交⊙O于F,连接AF,
则△CEB∽△AEF,
∴![]() ,
,
∵EF=2R-2=6,
∴![]()
∴BE=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目





