题目内容
【题目】如图,∠AOB=90°,OM平分∠AOB,将直角三角板的顶点P在射线OM上移动,两直角边分别与OA、OB相交于点C、D,问PC与PD相等吗?试说明理由.

【答案】PC与PD相等.
【解析】
先过点P作PE⊥OA于点E,PF⊥OB于点F,构造全等三角形:Rt△PCE和Rt△PDF,这两个三角形已具备两个条件:90°的角以及PE=PF,只需再证∠EPC=∠FPD,根据已知,两个角都等于90°减去∠CPF,那么三角形全等就可证.
PC与PD相等.理由如下:
过点P作PE⊥OA于点E,PF⊥OB于点F.

∵OM平分∠AOB,点P在OM上,PE⊥OA,PF⊥OB,
∴PE=PF(角平分线上的点到角两边的距离相等)
又∵∠AOB=90°,∠PEO=∠PFO=90°,
∴四边形OEPF为矩形,
∴∠EPF=90°,
∴∠EPC+∠CPF=90°,
又∵∠CPD=90°,
∴∠CPF+∠FPD=90°,
∴∠EPC=∠FPD=90°-∠CPF.
在△PCE与△PDF中,
∵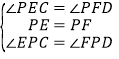 ,
,
∴△PCE≌△PDF(ASA),
∴PC=PD.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目