题目内容
【题目】如图，有一个边长不定的正方形ABCD，它的两个相对的顶点A，C分别在边长为1的正六边形一组平行的对边上，另外两个顶点B，D在正六边形内部（包括边界），则正方形边长a的取值范围是 ．
【答案】
≤a≤
．
【解析】
试题因为AC为对角线，故当AC最小时，正方形边长此时最小.
①当A、C都在对边中点时（如下图所示位置时），显然AC取得最小值，
∵正六边形的边长为1，
∴AC=
,
∴a2+a2=AC2=
.
∴a=
=.
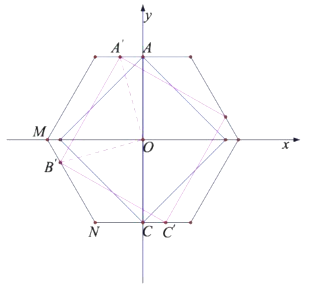
②当正方形四个顶点都在正六边形的边上时，a最大（如下图所示）.
设A′（t,
）时，正方形边长最大.
∵OB′⊥OA′.
∴B′（-，t）
设直线MN解析式为：y=kx+b,M（-1，0），N（-
，-）（如下图）
∴
.
∴
.
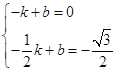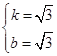∴直线MN的解析式为：y=（x+1）,
将B′（-，t）代入得：t=
-.
此时正方形边长为A′B′取最大.
∴a=
=3-.
故答案为：
.
练习册系列答案
优百分课时互动系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
相关题目
