题目内容
【题目】如图,在平面直角坐标系xOy中,已知正比例函数![]() 与一次函数
与一次函数![]() 的图像交于点A.
的图像交于点A.
(1)求点A的坐标;
(2)设x轴上一点P(a,b),过点P作x轴的垂线(垂线位于点A的右侧),分别交![]() 和
和![]() 的图像于点B、C,连接OC,若BC=
的图像于点B、C,连接OC,若BC=![]() OA,求△OBC的面积.
OA,求△OBC的面积.

【答案】(1)A(4,3);(2)28.
【解析】试题分析:(1)点A是正比例函数![]() 与一次函数
与一次函数![]() 图像的交点坐标,把
图像的交点坐标,把![]() 与
与![]() 联立组成方程组,方程组的解就是点A的横纵坐标;(2)过点A作x轴的垂线,在Rt△OAD中,由勾股定理求得OA的长,再由BC=
联立组成方程组,方程组的解就是点A的横纵坐标;(2)过点A作x轴的垂线,在Rt△OAD中,由勾股定理求得OA的长,再由BC=![]() OA求得OB的长,用点P的横坐标a表示出点B、C的坐标,利用BC的长求得a值,根据
OA求得OB的长,用点P的横坐标a表示出点B、C的坐标,利用BC的长求得a值,根据![]() 即可求得△OBC的面积.
即可求得△OBC的面积.
试题解析:解:(1)由题意得,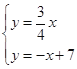 ,解得
,解得![]() ,
,
∴点A的坐标为(4,3).
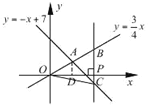
过点A作x轴的垂线,垂足为D,在Rt△OAD中,由勾股定理得,
![]() ,
,
∴![]() .
.
∵P(a,0),∴B(a,![]() ),C(a,-a+7),∴BC=
),C(a,-a+7),∴BC=![]() ,
,
∴![]() ,解得a=8.
,解得a=8.
∴![]() .
.

练习册系列答案
相关题目