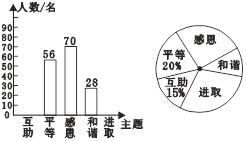题目内容
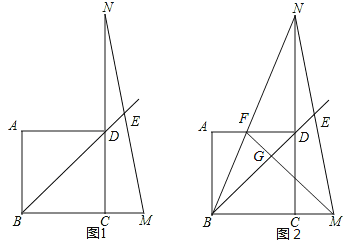
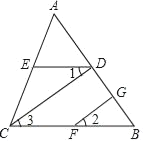
【题目】两个三角板ABC,DEF按如图所示的位置摆放,点B与点D重合,边AB与边DE在同一条直线上(假设图形中所有的点、线都在同一平面内),其中,∠C=∠DEF=90°,∠ABC=∠F=30°,AC=DE=4 cm.现固定三角板DEF,将三角板ABC沿射线DE方向平移,当点C落在边EF上时停止运动.设三角板平移的距离为![]() (cm),两个三角板重叠部分的面积为
(cm),两个三角板重叠部分的面积为![]() (cm2).
(cm2).
(1)当点C落在边EF上时,![]() =________cm;
=________cm;
(2)求![]() 关于
关于![]() 的函数表达式,并写出自变量
的函数表达式,并写出自变量![]() 的取值范围;
的取值范围;
(3)设边BC的中点为点M,边DF的中点为点N,直接写出在三角板平移过程中,点M与点N之间距离的最小值.
【答案】(1)10;(2)见解析;(3)![]() .
.
【解析】(1)由锐角三角函数,得到BG的长,进而得出GE的长,又矩形的性质可求解;
(2)分类讨论:①当0≤t<4时,根据三角形的面积公式可得答案;②当4≤t<8时,③当![]() 时,根据面积的和差求解;
时,根据面积的和差求解;
(3)根据点与直线上所有点的连线中垂线段最短,可得M在线段NG上,根据三角形的中位线,可得NG的长,根据锐角三角函数,可得MG的长,然后根据线段的和差求解.
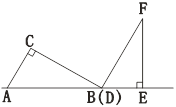
详解:(1)如图:
作CG⊥AB于G点.
在Rt△ABC中,由AC=4,∠ABC=30,得
BC=![]() =4
=4![]() .
.
在Rt△BCG中,BG=BCcos30°=6.
四边形CGEH是矩形,
CH=GE=BG+BE=6+4=10cm,
故答案为:10 .
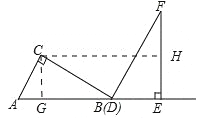
(2)①当![]() 时,如解图
时,如解图

∵∠GDB=60°,∠GBD=30°,
∴DB=x,DG=x,BG=![]() x,
x,
重叠部分的面积y=DG·BG=×x×![]() x=
x=![]() x2
x2
②![]() 时,如解图
时,如解图

BD=x,DG=x,BG=![]() x,BE=x-4,
x,BE=x-4,
EH=![]() (x-4)
(x-4)
重叠部分的面积y=S△BDG-S△BEH=DG·BG-BE·EH,
即y=×x×![]() x- (x-4)×
x- (x-4)×![]() (x-4),
(x-4),
化简得:![]()
③当![]() 时,如解图
时,如解图

AC=4,BC=4![]() ,BD=x,BE=x-4,
,BD=x,BE=x-4,
EG=![]() (x-4)
(x-4)
重叠部分的面积y=S△ABC-S△BEG=AC·BC-BE·EG,
即y=×4×4![]() - (x-4)×
- (x-4)×![]() (x-4),
(x-4),
化简得:![]()
综上所述,
(3) ![]()

【题目】随着我市社会经济的发展和交通状况的改善,我市的旅游业得到了高速发展,某旅游公司对我市一企业个人旅游年消费情况进行问卷调查,随机抽查部分员工,记录每个人年消费金额,并将调查数据适当整理,绘制成尚不完整的表和图(如图).
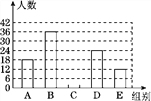
组别 | 个人年消费金额x/元 | 频数(人数) | 频率 |
A | x≤2 000 | 18 | 0.15 |
B | 2 000<x≤4 000 | a | b |
C | 4 000<x≤6 000 | ||
D | 6 000<x≤8 000 | 24 | 0.20 |
E | x>8 000 | 12 | 0.10 |
合计 | c | 1.00 |
根据以上信息回答下列问题:
(1)a=________,b=________,c=________,并将条形统计图补充完整;
(2)在这次调查中,个人年消费金额的中位数出现在________组;
(3)若这个企业有3 000名员工,请你估计个人旅游年消费金额在6 000元以上的人数.