题目内容
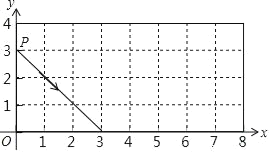
【题目】如图,抛物线![]() 与两坐标轴相交于点
与两坐标轴相交于点![]() ,
,![]() 是抛物线的顶点,
是抛物线的顶点, ![]() 是线段
是线段![]() 的中点.
的中点.
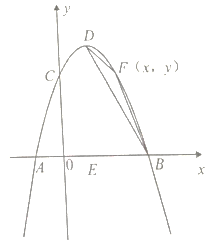
(1)求抛物线的解析式,并写出![]() 点的坐标;
点的坐标;
(2) ![]() 是抛物线上的动点;
是抛物线上的动点;
①当![]() 时,求
时,求![]() 的面积的最大值;
的面积的最大值;
②当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
【答案】(1)y=-x2+2x+3,D(1,4); (2) ①当x=2时,S最大值=1;②F(-![]() ,-2
,-2![]() -2)或(2-
-2)或(2-![]() ,-2+2
,-2+2![]() )
)
【解析】(1)利用待定系数法可求得抛物线的解析式,然后再配方成顶点式即可得点D的坐标;
(2)①由x>1,y>0,可以确定点F是直线BD上方抛物线上的动点,F(x, -x2+2x+3),过点F作FH⊥x轴交直线BD于M,由B、D的坐标易得yBD=-2x+6,继而得M(x,-2x+6),从而得到FM=-(x-2)2+1,再根据S△BDF=S△DFM+S△BFM,从而可得S△BDF=-(x-2)2+1,根据二次函数的性质即可得;
②分点F在x轴上方抛物线上,点F在x轴下方、y轴左侧抛物线上两种情况进行讨论即可得.
(1)抛物线![]() 与两坐标轴相交于点
与两坐标轴相交于点![]()
由题意得: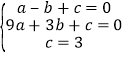 ,解得:
,解得: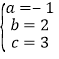 ,
,
所以抛物线的解析式为:y=-x2+2x+3,
配方得 y=-(x-1)2+4,∴抛物线顶点D的坐标为(1,4);
(2) ①∵x>1,y>0,
∴点F是直线BD上方抛物线上的动点,
则F(x, -x2+2x+3),
如图,过点F作FH⊥x轴交直线BD于M,
∵B(3,0), D(1,4),
∴yBD=-2x+6,
则M(x,-2x+6),
∴FM=-x2+2x+3-(-2x+6)= -x2+4x-3=-(x-2)2+1,
∵S△BDF=S△DFM+S△BFM,
∴S△BDF=![]() FM(x-1)+
FM(x-1)+![]() FM(3-x)=
FM(3-x)=![]() FM(x-1+3-x)=FM =-(x-2)2+1,
FM(x-1+3-x)=FM =-(x-2)2+1,
∴当x=2时,S最大值=1;
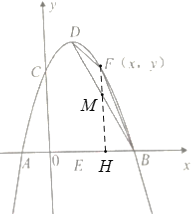
②如图,当 FE∥BD,且点F在x轴上方抛物线上时,
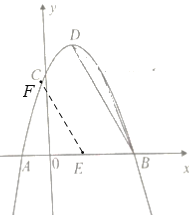
设FE的解析式为y=-2x+b,
∵直线FE过点E(1,0),
∴b=2,
yFE=-2x+2,
联立y=-2x+2与y=-x2+2x+3,
解得F(2-![]() ,-2+2
,-2+2![]() );
);
如图,当F在x轴下方、y轴左侧抛物线上时,设直线EF与直线BD交于点N,
∵∠AEF=∠NEB,
又∵∠AEF=∠
∴∠NEB=∠DBE,
∴NE=NB,
∴点N的横坐标为2,
又∵点N在直线yBD=-2x+6上,
∴N(2,2),
∴yEN=2x-2,
联立y=2x-2与y=-x2+2x+3,
解得F(-![]() ,-2
,-2![]() -2),
-2),
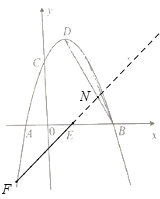
综上所述F(-![]() ,-2
,-2![]() -2)或(2-
-2)或(2-![]() ,-2+2
,-2+2![]() ).
).