题目内容
【题目】如图，在△ABC中，CD⊥AB于D，FG⊥AB于G，ED∥BC，求证∠1＝∠2．以下是推理过程，请你填空：
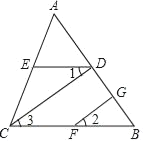
解：∵CD⊥AB，FG⊥AB
∴∠CDB＝∠FGB＝90°（ 垂直定义）
∴ ∥FG（ ）
∴ ＝∠3 （ ）
又∵DE∥BC （ 已知 ）
∴∠ ＝∠3 （ 两直线平行，内错角相等 ）
∴∠1＝∠2 （ ）
【答案】CD；同位角相等，两直线平行；∠2；两直线平行，同位角相等；1；等量代换
【解析】
利用平行线的判定与性质判断即可．
解：∵CD⊥AB，FG⊥AB
∴∠CDB=∠FGB=90°（ 垂直定义）
∴CD∥FG（同位角相等，两直线平行）
∴∠2=∠3（两直线平行，同位角相等）
又∵DE∥BC （已知）
∴∠1=∠3（两直线平行，内错角相等）
∴∠1=∠2（等量代换）.
故答案为：CD；同位角相等，两直线平行；∠2；两直线平行，同位角相等；1；等量代换.
练习册系列答案
名校课堂系列答案
相关题目
