Question

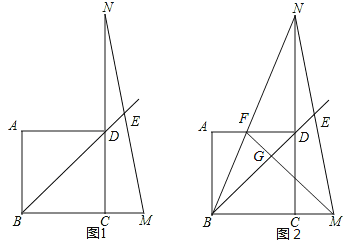
【题目】如图1，在正方形ABCD中，延长BC至M，使BM=DN，连接MN交BD延长线于点E．

（1）求证：BD+2DE=BM．

（2）如图2，连接BN交AD于点F，连接MF交BD于点G．若AF：FD=1：2，且CM=2，则线段DG= ．

Answer 1

【答案】（1）证明见解析；（2）．

【解析】试题（1）根据结论可以猜想：要想解决问题需要把BD+2DE和BM转化到等腰直角三角形中去，因此想到过点M作BM的垂线与BD 的延长线交于点P，然后利用全等三角形的性质证明DE=PE即可证出结论；（2）由AB//CN可得：，所以DN=BM=2AB=2BC，又CM=2，所以BC=AD=CM=2，所以BD=，FD=，由AD//BM可得：，所以，因为BD=，所以DG=．

试题解析：（1）证明：过点M作NPBM，交BD 的延长线交于点P，

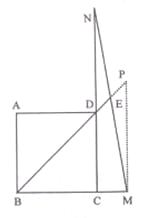
因为四边形ABCD是正方形，所以∠BCD =90°，∠DBC=∠BDC=45°，

所以PM∥CN，所以∠N=∠EMP，∠BDC=∠MPB=45°，

所以∠DBC=∠MPB，所以BM=MP，又因为BM=DN，所以DN=MP，

又因为∠N=∠EMP，∠NED=∠MEP，所以△NDE≌△MPE，所以DE=EP

由勾股定理可得：BP=BM，即BD+2DE=BM

（2）DG=