Question

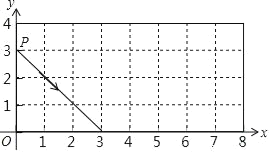
【题目】如图，抛物线与直线交于C，D两点，其中点C在y轴上，点D的坐标为。点P是y轴右侧的抛物线上一动点，过点P作PE⊥x轴于点E，交CD于点F.

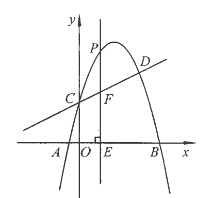
（1）求抛物线的解析式；

（2）若点P的横坐标为m，当m为何值时，以O，C，P，F为顶点的四边形是平行四边形？请说明理由；

（3）若存在点P，使∠PCF=450，请直接写出相应的点P的坐标。

Answer 1

【答案】（1）（2）平行四边形（3）P（）或（）

【解析】解：（1）∵直线经过点C，∴C（0，2）。

∵抛物线经过点C（0，2），D ，

∴，解得。

∴抛物线的解析式为。

（2）∵点P的横坐标为m且在抛物线上，

∴。

∵PF∥CO，∴当PF=CO时，以O，C，P，F为顶点的四边形是平行四边形。

当时，，

∴，解得：。

即当m=1或2时，四边形OCPF是平行四边形。

当时，，

∴，解得：（∵点P在y轴右侧的抛物线上，∴舍去）

即当时，四边形OCFP是平行四边形。

综上所述，当m=1或2或时，以O，C，P，F为顶点的四边形是平行四边形。

（3）P（）或（）。

（1）由直线经过点C，求出点C的坐标；由抛物线经过点C，D两点，用待定系数法即可求出抛物线的解析式。

（2）因为PF∥CO，所以当PF=CO时，以O，C，P，F为顶点的四边形是平行四边形，分和两种情况讨论即可。

（3）如图，当点P在CD上方且∠PCF=450时，

作PM⊥CD于点M，CN⊥PF于点N，则△PMF∽△CNF，

∴。∴PM=CM=2CF。

∴。

又∵，∴。

解得：，（舍去）。

∴P（）。

当点P在CD下方且∠PCF=450时，

同理可以求得：另外一点为P（）。