题目内容
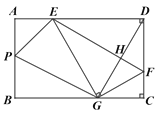
【题目】如图,正方形![]() 中,
中,![]() ,
,![]() 是
是![]() 边的中点,点
边的中点,点![]() 是正方形内一动点,
是正方形内一动点,![]() ,连接
,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得
得![]() ,连接
,连接![]() ,
,![]() .
.
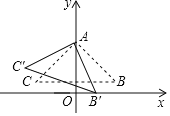
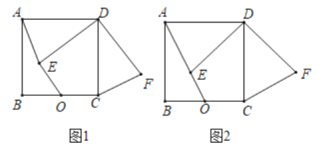
(1)如图1,求证:![]() ;
;
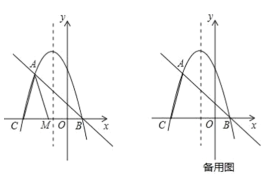
(2)如图2,若![]() ,
,![]() ,
,![]() 三点共线,求点
三点共线,求点![]() 到直线
到直线![]() 的距离.
的距离.
【答案】(1)证明见解析;(2)点F到直线BC的距离是![]() .
.
【解析】
(1)由旋转的性质可得∠EDF=90°,DE=DF,由正方形的性质可得∠ADC=90°,DE=DF,可得∠ADE=∠CDF,由“SAS”可证△ADE≌△CDF,可得AE=CF;
(2)由勾股定理可求AO的长,可得AE=CF=3,通过证明△ABO∽△CPF,可得![]() ,即可求PF的长,即可求点F到直线BC的距离.
,即可求PF的长,即可求点F到直线BC的距离.
解:(1)由旋转得:![]() ,
,![]() ,
,

∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
∵ ,
,
∴![]() ,
,
∴![]() ;
;
(2)解:如图2,过点F作FP⊥BC交BC延长线于点P,
则线段FP的长度就是点F到直线BC的距离.

∵点O是BC中点,且AB=BC=2![]()
∴BO=![]() ,
,
∴AO=![]() =5
=5
∵OE=2
∴AE=AO-OE=3
∵△ADE≌△CDF
∴AE=CF=3,∠DAO=∠DCF
∴∠BAO=∠FCP,且∠ABO=∠FPC=90°
∴△ABO∽△CPF
∴![]()
∴![]()
∴PF=![]()
∴点F到直线BC的距离为![]() .
.

练习册系列答案
相关题目