Question

【题目】在平面直角坐标系中，我们定义直线y=ax﹣a为抛物线y=ax2+bx+c（a、b、c为常数，a≠0）的“梦想直线”；有一个顶点在抛物线上，另有一个顶点在y轴上的三角形为其“梦想三角形”．

已知抛物线与其“梦想直线”交于A、B两点（点A在点B的左侧），与x轴负半轴交于点C．

（1）填空：该抛物线的“梦想直线”的解析式为 ，

（2）如图，点M为线段CB上一动点，将△ACM以AM所在直线为对称轴翻折，点C的对称点为N，若△AMN为该抛物线的“梦想三角形”，求点N的坐标；

（3）当点E在抛物线的对称轴上运动时，在该抛物线的“梦想直线”上，是否存在点F，使得以点A、C、E、F为顶点的四边形为平行四边形？若存在，请直接写出点E、F的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）y＝x＋（2）N点坐标为（0，23）或（，）（3）满足条件的点F，此时E（1，）、F（0，）或E（1，），F（4，）．

【解析】

（1）由梦想直线的定义可求得其解析式；

（2）当N点在y轴上时，过A作AD⊥y轴于点D，则可知AN＝AC，结合A点坐标，则可求得ON的长，可求得N点坐标；当M点在y轴上即，M点在原点时，过N作NP⊥x轴于点P，由条件可求得∠NMP＝60°，在Rt△NMP中，可求得MP和NP的长，则可求得N点坐标；

（3）当AC为平行四边形的一边时，过F作对称轴的垂线FH，过A作AK⊥x轴于点K，可证△EFH≌△ACK，可求得DF的长，则可求得F点的横坐标，从而可求得F点坐标，由HE的长可求得E点坐标；当AC为平行四边形的对角线时，设E（1，t），由A、C的坐标可表示出AC中点，从而可表示出F点的坐标，代入直线AB的解析式可求得t的值，可求得E、F的坐标．

（1）∵抛物线，

∴其梦想直线的解析式为y＝x＋

故答案为：y＝x＋；

（2）联立梦想直线与抛物线解析式可得，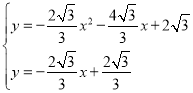

解得或，

∴A（2，2），B（1，/span>0），

当点N在y轴上时，△AMN为梦想三角形，

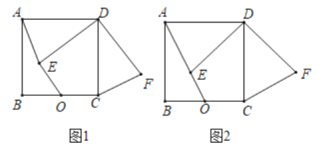
如图1，过A作AD⊥y轴于点D，则AD＝2，

在中，令y＝0可求得x＝3或x＝1，

∴C（3，0），且A（2，2），

∴AC＝，

由翻折的性质可知AN＝AC＝，

在Rt△AND中，由勾股定理可得DN＝＝＝3，

∵OD＝2，

∴ON＝23或ON＝2＋3，

当ON＝2＋3时，则MN＞OD＞CM，与MN＝CM矛盾，不合题意，

∴N点坐标为（0，23）；

当M点在y轴上时，则M与O重合，过N作NP⊥x轴于点P，如图2，

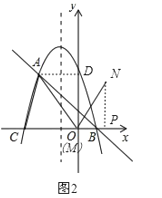
在Rt△AMD中，AD＝2，OD＝2，

∴tan∠DAM＝＝3，

∴∠DAM＝60°，

∵AD∥x轴，

∴∠AMC＝∠DAO＝60°，

又由折叠可知∠NMA＝∠AMC＝60°，

∴∠NMP＝60°，且MN＝CM＝3，

∴MP＝MN＝，NP＝MNsin60°=MN＝，

∴此时N点坐标为（，）；

综上可知N点坐标为（0，23）或（，）；

（3）①当AC为平行四边形的边时，如图2，过F作对称轴的垂线FH，过A作AK⊥x轴于点K，

则有AC∥EF且AC＝EF，

∴∠ACK＝∠EFH，

在△ACK和△EFH中

∴△ACK≌△EFH（AAS），

∴FH＝CK＝1，HE＝AK＝2，

∵抛物线对称轴为x＝1，

∴F点的横坐标为0或2，

∵点F在直线AB上，

∴当F点横坐标为0时，则F（0，），此时点E在直线AB下方，

∴E到x轴的距离为EHOF＝2＝，即E点纵坐标为，

∴E（1，）；

当F点的横坐标为2时，则F与A重合，不合题意，舍去；

②当AC为平行四边形的对角线时，

∵C（3，0），且A（2，2），

∴线段AC的中点坐标为（2.5，），

设E（1，t），F（x，y），

则x1＝2×（2.5），y＋t＝2，

∴x＝4，y＝2t，

代入直线AB解析式可得2t＝×（4）＋，解得t＝，

∴E（1，），F（4，）；

综上可知存在满足条件的点F，此时E（1，）、F（0，）或E（1，），F（4，）．