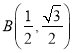题目内容
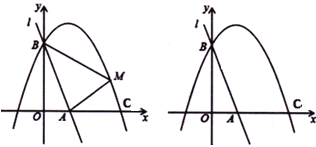
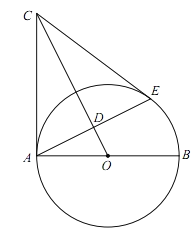
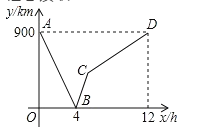
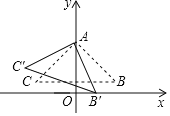
【题目】如图,在Rt△ABC中,∠CAB=90°,AB=AC,点A在y轴上,BC∥x轴,点B![]() .将△ABC绕点A顺时针旋转的△AB′C′,当点B′落在x轴的正半轴上时,点C′的坐标为( )
.将△ABC绕点A顺时针旋转的△AB′C′,当点B′落在x轴的正半轴上时,点C′的坐标为( )
A.(﹣![]() ,
,![]() ﹣1)B.(﹣
﹣1)B.(﹣![]() ,
,![]() ﹣1)
﹣1)
C.(﹣![]() ,
,![]() +1)D.(﹣
+1)D.(﹣![]() ,
,![]() ﹣1)
﹣1)
【答案】D
【解析】
作C'D⊥OA于D,设AO交BC于E,由等腰直角三角形的性质得出∠B=45°,AE=![]() BC=
BC=![]() ,BC=2
,BC=2![]() =
=![]() AB,得出AB=2,OA=
AB,得出AB=2,OA=![]() ,由旋转的性质得:AB'=AB=AC=AC'=2,∠C'AB'=∠CAB=90°,由勾股定理得出OB'=
,由旋转的性质得:AB'=AB=AC=AC'=2,∠C'AB'=∠CAB=90°,由勾股定理得出OB'=![]() =1=
=1=![]() AB',证出∠OAB'=30°,得出∠C'AD=∠AB'O=60°,证明△AC'D≌△B'AO得出AD=OB'=1,C'D=AO=
AB',证出∠OAB'=30°,得出∠C'AD=∠AB'O=60°,证明△AC'D≌△B'AO得出AD=OB'=1,C'D=AO=![]() ,求出OD=AO﹣AD=
,求出OD=AO﹣AD=![]() ﹣1,即可得出答案.
﹣1,即可得出答案.
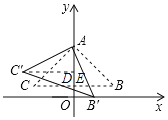
解:作C'D⊥OA于D,设AO交BC于E,如图所示:
则∠C'DA=90°,
∵∠CAB=90°,AB=AC,
∴△ABC是等腰直角三角形,
∴∠B=45°,
∵BC∥x轴,点B(![]() ,
,![]() ﹣
﹣![]() ),
),
∴AE=![]() BC=
BC=![]() ,BC=2
,BC=2![]() =
=![]() AB,
AB,
∴AB=2,OA=![]() ,
,
由旋转的性质得:AB'=AB=AC=AC'=2,∠C'AB'=∠CAB=90°,
∴OB'=![]() =1=
=1=![]() AB',
AB',
∴∠OAB'=30°,
∴∠C'AD=∠AB'O=60°,
在△AC'D和△AB'O中,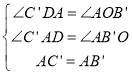 ,
,
∴△AC'D≌△B'AO(AAS),
∴AD=OB'=1,C'D=AO=![]() ,
,
∴OD=AO﹣AD=![]() ﹣1,
﹣1,
∴点C′的坐标为(﹣![]() ,
,![]() ﹣1);
﹣1);
故选:D.

练习册系列答案
相关题目