题目内容
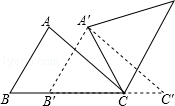
如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=3,将△ABC沿AC边所在直线向右平移x个单位,记平移后的对应三角形为△DEF,连接BE.
(1)当x=4时,求四边形ABED的周长;
(2)当x为何值时,△BED是等腰三角形?

(1)当x=4时,求四边形ABED的周长;
(2)当x为何值时,△BED是等腰三角形?

(1)16
(2)当x为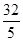 或2.5或4时,△BED是等腰三角形
或2.5或4时,△BED是等腰三角形
(2)当x为
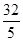 或2.5或4时,△BED是等腰三角形
或2.5或4时,△BED是等腰三角形解:(1)将△ABC沿AC边所在直线向右平移x个单位,当x=4时,
即AD=4,又因为平移后的对应三角形为△DEF,
所以,AB=AD=DE=BE=4,
所以四边形ABED的周长为16.
(2)当BE=ED=4时,x=4;
当BE=BD=x时,由∠CDE=∠BDE,BC⊥DE,
利用轴对称的性质可得DC=BD=BE,即5﹣x=x,
x=2.5,
当BD=ED=4时,
过点D作DH⊥BE于H,
BH=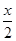 ,DH=
,DH=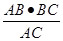 =
=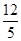 ,
,
利用勾股定理得:DH2+BH2=BD2,
即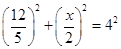 ,
,
x=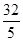 .
.
答:(1)当x=4时,求四边形ABED的周长为16;(2)当x为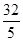 或2.5或4时,△BED是等腰三角形.
或2.5或4时,△BED是等腰三角形.

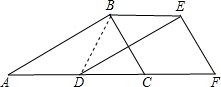
(1)根据轴对称的性质,求得AD,DE的长,然后即可求四边形ABED的周长
(2)分两种情况:一是,当BE=ED=4时,利用轴对称的性质可得x的值,二是当BD=ED=4时,利用勾股定理可求得x的值.
即AD=4,又因为平移后的对应三角形为△DEF,
所以,AB=AD=DE=BE=4,
所以四边形ABED的周长为16.
(2)当BE=ED=4时,x=4;
当BE=BD=x时,由∠CDE=∠BDE,BC⊥DE,
利用轴对称的性质可得DC=BD=BE,即5﹣x=x,
x=2.5,
当BD=ED=4时,
过点D作DH⊥BE于H,
BH=
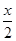 ,DH=
,DH=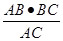 =
=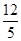 ,
,利用勾股定理得:DH2+BH2=BD2,
即
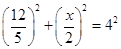 ,
,x=
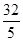 .
.答:(1)当x=4时,求四边形ABED的周长为16;(2)当x为
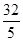 或2.5或4时,△BED是等腰三角形.
或2.5或4时,△BED是等腰三角形.

(1)根据轴对称的性质,求得AD,DE的长,然后即可求四边形ABED的周长
(2)分两种情况:一是,当BE=ED=4时,利用轴对称的性质可得x的值,二是当BD=ED=4时,利用勾股定理可求得x的值.

练习册系列答案
相关题目

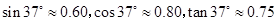 ).
).