题目内容
【题目】如图,直线y=-![]() x+2
x+2![]() 与x轴、y轴分别相交于A、B两点,圆心P的坐标为(-2,0),⊙P与y轴相切于点O.若将⊙P沿x轴向右移动,当⊙P与该直线相交时,满足横坐标为整数的点P的个数是( )
与x轴、y轴分别相交于A、B两点,圆心P的坐标为(-2,0),⊙P与y轴相切于点O.若将⊙P沿x轴向右移动,当⊙P与该直线相交时,满足横坐标为整数的点P的个数是( )
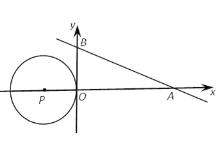
A. 3 B. 4 C. 5 D. 7
【答案】D
【解析】
根据直线与坐标轴的交点,得出A,B的坐标,再利用三角形相似得出圆与直线相切时的坐标,进而得出相交时的坐标.
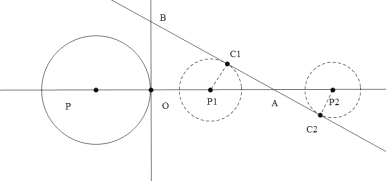
如图
∵直线y=-![]() x+2
x+2![]() 与x轴、y轴分别相交于A、B两点,圆心P的坐标为(-2,0),
与x轴、y轴分别相交于A、B两点,圆心P的坐标为(-2,0),
∴A点的坐标为0=-![]() x+2
x+2![]()
x=6, A(6,0),
B点的坐标为:(0,2![]() ),
),
∴AB=4![]()
将圆P沿x轴向左移动,当圆P与该直线相切于C1 时,P1C1 =2,
根据△AP1C1∽△ABO,![]() ∴AP 1 =4,
∴AP 1 =4,
∴P 1 的坐标为:(2,0),
将圆P沿x轴向左移动,当圆P与该直线相切于C2 时,P2C2 =2,
根据△AP2C2∽△ABO,![]() ∴AP2 =4,
∴AP2 =4,
P2 的坐标为:(10,0),
从2到10,当⊙P与该直线相交时,整数点有,3,4,5,6,7,8,9故横坐标为整数的点P的个数是7个
故选D

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目