题目内容
【题目】在△ABC中,AB=AC,点D在直线BC上(不与点B、C重合),线段AD绕A点逆时针方向旋转∠BAC的大小,得线段AE,连接DE、CE.探索∠BCE与∠BAC的大小关系,并加以证明.

【答案】见解析.
【解析】
分类讨论:
当点D在线段BC上,如图1,根据旋转的性质得AD=AE,再由∠DAE=∠BAC得到∠BAD=∠CAE,则可根据SAS判定△ABD≌△ACE,得到∠ABC=∠ACE,而∠BCE=∠BCA+∠ACE=∠BCA+∠ABC,而∠BAC+∠BCA+∠ABC=180°,于是得到∠BCE+∠BAC=180°;
当点D再BC的延长线上,如图2,同样可证明△ABD≌△ACE,得到∠ABD=∠ACE,同样可得∠BCE+∠BAC=180°;
当点D再CB延长线上时,如图3,同样可证明△ABD≌△ACE,得到∠ABD=∠ACE,根据三角形外角性质得∠ABD=∠BAC+∠ACB,∠ACE=∠ACB+∠BCE,所以∠BCE=∠BAC;
综上所述,∠BCE与∠BAC相等或互补.
∠BCE与∠BAC相等或互补.
理由如下:
当点D在线段BC上,如图1,
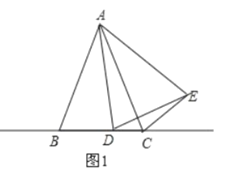
∵线段AD绕点A按逆时针方向旋转得到AE
∴AD=AE
∵∠DAE=∠BAC
∴∠BAD=∠CAE
在△ABD和△ACE中
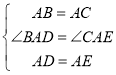
∴△ABD≌△ACE(SAS)
∴∠ABC=ACE
∴∠BCE=∠BCA+∠ACE=∠BCA+∠ABC
∵∠BAC+∠BCA+∠ABC=180°
∴∠BCE+∠BAC=180°
当点D再BC的延长线上,如图2,
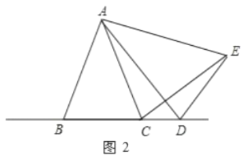
同样可证明△ABD≌△ACE,得到∠ABD=ACE
同样得到∠BCE+∠BAC=180°
当点D再CB延长线上时,如图3,
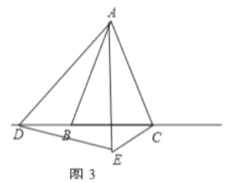
同样可证明△ABD≌△ACE,得到∠ABD=ACE
∵∠ABD=∠BAC+∠ACB
∠ACE=∠ACB+∠BCE
∴∠BCE=∠BAC
综上所述,∠BCE与∠BAC相等或互补.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案