Question

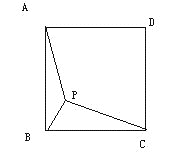
【题目】如图,P是正方形ABCD内一点，∠APB=135 ， BP=1，AP=，求PC的值（　　）

A. B. 3 C. D. 2

Answer 1

【答案】B

【解析】

把△PBC绕点B逆时针旋转90°得到△ABP′，根据旋转的性质可得AP′=PC，BP′=BP，△PBP′是等腰直角三角形，利用勾股定理求出PP′，然后求出∠APP′=90°，再利用勾股定理列式计算求出P′A，从而得解．

如图，把△PBC绕点B逆时针旋转90°得到△ABP′（点C的对应点C′与点A重合），

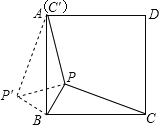
所以，AP′=PC，BP′=BP=1，

所以，△PBP′是等腰直角三角形，

所以，∠P′PB=45°，PP′=，

∵∠APB=135°，

∴∠APP′=∠APB-∠P′PB=135°-45°=90°，

在Rt△APP′中，AP′=，

∴PC=AP′=3，

故选B．