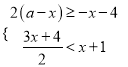��Ŀ����
����Ŀ����ͼ�٣���֪AB��CD����E��F�ֱ���AB��CD�ϵĵ㣬��P����ƽ����֮���һ�㣬���AEP=������PFC=������ͼ���У�����E������EH��CD�ڵ�N��������FI���ӳ�PF��G��ʹ��PE��FG�ֱ�ƽ�֡�AEH����DFl���õ�ͼ����
��1����ͼ���У�����P��PM��AB������=20�㣬��=50��ʱ����EPM=�� ���ȣ���EPF=�� ���ȣ�
��2���ڣ�1���������£���ͼ���С�END���CFI�Ķ�����
��3����ͼ���У���FI��EHʱ����ֱ��д����������������ϵ��

���𰸡���1��20��70����2��80�㣻��3��90�㣻
��������
��1����PM��AB������ֱ��ƽ�У��ڴ�����ȿɵá�EPM=��AEP=20�㣬����ƽ�й��������ۿɵ�PM��CD���̶��ɵá�MPF=��CFP=50�㣬�Ӷ�������á�EPF��
��2���ɽ�ƽ���ߵĶ���ɵá�AEH=2��=40�㣬�ٸ���AD��BC������ֱ��ƽ�У��ڴ�����ȿɵá�END=��AEH=40�㣬�ɶԶ�������Լ���ƽ���߶���ɵá�IFG=��DFG=��=50�㣬�ٸ���ƽ�Ƕ��弴����á�CFI�Ķ�����
��3���ɣ�2���ɵã���CFI=180��-2�£���AB��CD���ɵá�END=2������FI��EHʱ����END=��CFI���ݴ˼��ɵ���+��=90�㣮
��1����PM��AB����=20�㣬
���EPM=��AEP=20�㣬
��AB��CD��PM��AB��
��PM��CD��
���MPF=��CFP=50�㣬
���EPF=20��+50��=70�㣬
�ʴ�Ϊ��20��70��
��2����PEƽ�֡�AEH��
���AEH=2��=40�㣬
��AD��BC��
���END=��AEH=40�㣬
�֡�FGƽ�֡�DFI��
���IFG=��DFG=��=50�㣬
���CFI=180��-2��=80�㣻
��3���ɣ�2���ɵã���CFI=180��-2�£�
��AB��CD��
���END=��AEN=2����
�൱FI��EHʱ����END=��CFI��
��2��=180��-2�£�
����+��=90�㣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ������ABC�У�AB=AC����E��F�ֱ���AB��AC�ϣ�AE=AF��BF��CE�ཻ�ڵ�P����֤��PB=PC����ֱ��д��ͼ��������ȵ��߶Σ�

����Ŀ������ij��ɫ�����߲˻����мס�������ֲ������������ֲ��A��B�����߲ˣ�����ֲ����ֲ�������߲˵���ֲ��������������±���
��ֲ�� | ��ֲA���߲��������λ��Ķ�� | ��ֲB���߲��������λ��Ķ�� | �����루��λ��Ԫ�� |
�� | 1 | 3 | 13500 |
�� | 2 | 2 | 13000 |
˵������ͬ��ֲ����ֲ��ͬ���߲�ÿĶƽ���������
��1����A��B�����߲�ÿĶƽ��������Ƕ���Ԫ��
��2������ס�������ֲ��������ֲ���ƻ�����50Ķ��������ֲA��B�����߲ˣ�Ϊ��ʹ�����벻����16400Ԫ����������ֲ��������ֲA���߲˶���Ķ��