题目内容
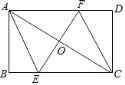
【题目】已知：如图，⊙O的半径OC垂直弦AB于点H，连接BC，过点A作弦AE∥BC，过点C作CD∥BA交EA延长线于点D，延长CO交AE于点F．
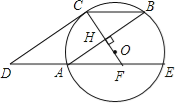
（1）求证：CD为⊙O的切线；
（2）若BC=5，AB=8，求OF的长．
【答案】（1）见解析；（2）
．
【解析】
试题(1)、根据平行线的性质进行判定；(2)、首先求出AH各BH的长度，根据平行线得出△HAF和△HBC全等，得出FH=CH=3，CF=6，然后设BO=x，则OH=x－3，根据Rt△BHO的勾股定理求出x的值，得出OF的长度.
试题解析：(1)、∵OC⊥AB，CD∥BA，∴CD⊥OC，∴CD为⊙O的切线，
(2)、OC⊥AB，AB＝8， ∴AH=BH=
=4
在Rt△BCH中，∵BH＝4，BC＝5，∴CH＝3， ∵AE∥BC，
∴∠HAF=∠HBC，又∠AHF=∠BHC，∴△HAF≌△HBC
∴FH=CH=3，CF=6
连接BO，设BO＝x，则OH＝x－3，
在Rt△BHO中，有
解得：x=
，∴OF=CF－OC=．
练习册系列答案
相关题目
