Question

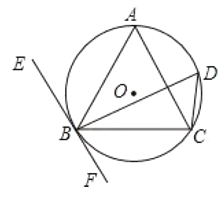
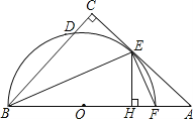
【题目】如图，在△ABC中，∠C=90°，∠ABC的平分线交AC于点E，过点E作BE的垂线交AB于点F，⊙O是△BEF的外接圆．

（1）求证：AC是⊙O的切线；

（2）过点E作EH⊥AB，垂足为H，求证：CD=HF；

（3）若CD=1，EF=，求AF长．

Answer 1

【答案】（1）见解析；（2）见解析；（3）

【解析】

（1）连接OE，由于BE是角平分线，则有∠CBE=∠OBE；而OB=OE，就有∠OBE=∠OEB，等量代换有∠OEB=∠CBE，那么利用内错角相等，两直线平行，可得OE∥BC；又∠C=90°，所以∠AEO=90°，即AC是⊙O的切线；

（2）连结DE，先根据AAS证明△CDE≌△HFE，再由全等三角形的对应边相等即可得出CD=HF；

（3）先证得△EHF∽△BEF，根据相似三角形的性质求得BF=10，进而根据直角三角形斜边中线的性质求得OE=5，进一步求得OH，然后解直角三角形即可求得OA，得出AF．

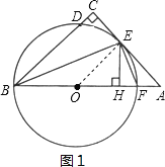
证明：（1）如图1，连接OE．

∵BE⊥EF，

∴∠BEF=90°，

∴BF是圆O的直径．

∵BE平分∠ABC，

∴∠CBE=∠OBE，

∵OB=OE，

∴∠OBE=∠OEB，

∴∠OEB=∠CBE，

∴OE//BC，

∴∠AEO=∠C=90°，

∴AC是⊙O的切线；

（2）解：如图2，连结DE．

∵∠CBE=∠OBE，EC⊥BC于C，EH⊥AB于H，

∴EC=EH．

∵∠CDE+∠BDE=180°，∠HFE+∠BDE=180°，

∴∠CDE=∠HFE．

在△CDE与△HFE中，，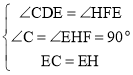

∴△CDE≌△HFE（AAS），

∴CD=HF．

（3）解：由（2）得CD=HF，又CD=1，

∴HF=1，

∵EF⊥BE，

∴∠BEF=90°，

∴∠EHF=∠BEF=90°，

∵∠EFH=∠BFE，

∴△EHF∽△BEF，

∴，即，

∴BF=10，

∴OE=BF=5，OH=5-1=4，

∴Rt△OHE中，cos∠EOA=，

∴Rt△EOA中，cos∠EOA=，

∴，

∴OA=，

∴AF=．