题目内容
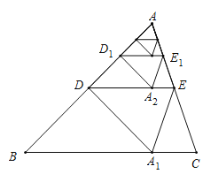
【题目】如图,在![]() 中,
中,![]() ,
,![]() 、
、![]() 是斜边
是斜边![]() 上两点,且
上两点,且![]() ,将
,将![]() 绕
绕![]() 顺时针旋转
顺时针旋转![]() 后,得到
后,得到![]() ,连接
,连接![]() ,则下列结论不正确的是( )
,则下列结论不正确的是( )
A.![]() B.
B.![]() 为等腰直角三角形
为等腰直角三角形
C.![]() 平分
平分![]() D.
D.![]()
【答案】B
【解析】
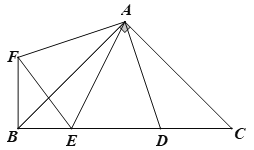
由已知![]() 和旋转的性质可判断A项,进一步可判断C项;利用SAS可证明△AED≌△AEF,可得ED=EF,容易证明△FBE是直角三角形,由此可判断D项和B项,于是可得答案.
和旋转的性质可判断A项,进一步可判断C项;利用SAS可证明△AED≌△AEF,可得ED=EF,容易证明△FBE是直角三角形,由此可判断D项和B项,于是可得答案.
解:∵△ADC绕点A顺时针旋转90°得△AFB,
∴△ADC≌△AFB,∠FAD=90°,AD=AF,
∵∠DAE=45°,
∴∠FAE=90°-∠DAE=45°,所以A正确;
∴∠DAE=∠FAE,
∴![]() 平分
平分![]() ,所以C正确;
,所以C正确;
∵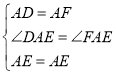
∴△AED≌△AEF(SAS),
∴ED=EF,
在Rt△ABC中,∠ABC+∠C=90°,
又∵∠C=∠ABF,
∴∠ABC+∠ABF=90°,即∠FBE=90°,
∴在Rt△FBE中,由勾股定理得:![]() ,
,
∴![]() ,所以D正确;
,所以D正确;
而BE、CD不一定相等,所以BE、BF不一定相等,所以B不正确.
故选B.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
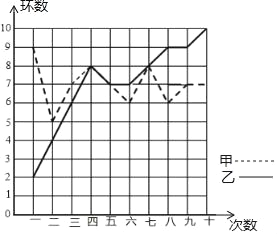
【题目】某市射击队甲、乙两名队员在相同的条件下各射耙10次,每次射耙的成绩情况如图所示:
(1)请将下表补充完整:(参考公式:方差S2=![]() [(x1﹣
[(x1﹣![]() )2+(x2﹣
)2+(x2﹣![]() )2+…+(xn﹣
)2+…+(xn﹣![]() )2])
)2])
平均数 | 方差 | 中位数 | |
甲 | 7 |
| 7 |
乙 |
| 5.4 |
|
(2)请从下列三个不同的角度对这次测试结果进行
①从平均数和方差相结合看, 的成绩好些;
②从平均数和中位数相结合看, 的成绩好些;
③若其他队选手最好成绩在9环左右,现要选一人参赛,你认为选谁参加,并说明理由.