题目内容
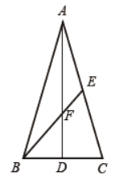
【题目】如图，在等腰
中，
，
、
分别是边
、
上的中线，与交于点
，若
，
，则的面积等于____________．
【答案】
【解析】
过E作EG⊥BC于G,根据已知条件得到点F是△ABC的重心,求得AD=3DF=9,根据等腰三角形的性质得到AD⊥BC,BD=CD,根据平行线分线段成比例定理得到EG=
,根据勾股定理得到BG=
，根据三角形的面积公式即可得到结论.
过E作EG⊥BC于G，
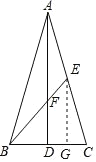
∵AD、BE分别是边BC、AC上的中线，
∴点F是△ABC的重心，
∴AD=3DF=9，
∵AB=AC，AD是边BC上的中线，
∴AD⊥BC，BD=CD，
∵BE是边AC上的中线，
∴AE=CE，
∵AD⊥BC，EG⊥BC，
∴EG∥AD，
∴EG=
∵BE=6，
∴BC=
∴BG=
，
∴△ABC的面积=
，
故答案为：.
练习册系列答案
教材全解字词句篇系列答案
相关题目
