Question

【题目】如图，长沙九龙仓国际金融中心主楼高达，是目前湖南省第一高楼，和它处于同一水平面上的第二高楼高，为了测量高楼上发射塔的高度，在楼底端点测得的仰角为α，，在顶端E测得A的仰角为，求发射塔的高度.

Answer 1

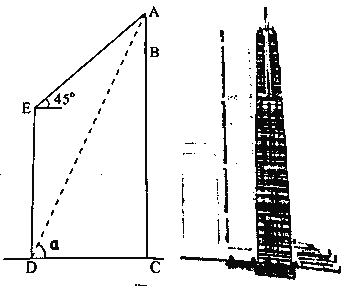
【答案】AB的高度为28米

【解析】设AB的高度为x米，过点E作EF⊥AC于F，则FC＝DE＝340米，继而可得BF＝112米，从而可得AF＝（112+x）米，在Rt△AEF中，根据等腰直角三角形的性质可得EF＝AF＝CD＝（112+x）米，Rt△ACD中，由sinａ= ，可得tanａ= ，再由tanａ＝得到关于x的方程，解方程即可求得AB的长.

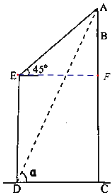
设AB的高度为x米，

如图，过点E作EF⊥AC于F，则FC＝DE＝340米，

∴BF＝452－340＝112米，

∴AF＝（112+x）米，

在Rt△AEF中，∠FAE＝∠AEF＝45°，

∴EF＝AF＝CD＝（112+x）米，

Rt△ACD中，sinａ= =，

设AC=24k，AD=25k(k>0)，由勾股定理则有CD==7k，

∴tanａ== ，

Rt△ACD中，AC=（452+x）米，tanａ＝=，

解得x=28，

答：发射塔AB的高度是28米..