题目内容
(8分 )A、B两
)A、B两 地相距630千米,客车、货车分别从A、B两地同时出发,匀速相向行驶.货车两小时可到达途中C站,客车需9小时到达C站(如图1所示).货车的速度是客车的
地相距630千米,客车、货车分别从A、B两地同时出发,匀速相向行驶.货车两小时可到达途中C站,客车需9小时到达C站(如图1所示).货车的速度是客车的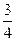 ,客、货车到C站的距离分别为y1、y2(千米),它们与行驶时间x(小
,客、货车到C站的距离分别为y1、y2(千米),它们与行驶时间x(小
时)之间的函数关系如图2所示.
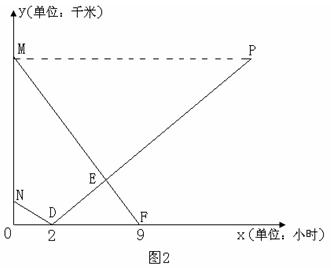
(1)求客、货两车的速度;
(2)求两小时后,货车到C站的距离y2与行驶时间x之间的函数关系式;
(3)如图2,两函数图象交于点E,求E点坐标,并说明它所表示的实际意义.
 )A、B两
)A、B两 地相距630千米,客车、货车分别从A、B两地同时出发,匀速相向行驶.货车两小时可到达途中C站,客车需9小时到达C站(如图1所示).货车的速度是客车的
地相距630千米,客车、货车分别从A、B两地同时出发,匀速相向行驶.货车两小时可到达途中C站,客车需9小时到达C站(如图1所示).货车的速度是客车的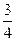 ,客、货车到C站的距离分别为y1、y2(千米),它们与行驶时间x(小
,客、货车到C站的距离分别为y1、y2(千米),它们与行驶时间x(小时)之间的函数关系如图2所示.

(1)求客、货两车的速度;
(2)求两小时后,货车到C站的距离y2与行驶时间x之间的函数关系式;
(3)如图2,两函数图象交于点E,求E点坐标,并说明它所表示的实际意义.
解:(1)设客车速度为v千米/时,则货车速度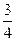 v千米/时,根据题意得
v千米/时,根据题意得
9v +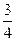 v ´2=630.……………………2分
v ´2=630.……………………2分
解得v=60.
答:客车速度为60v千米/时,慢车的速度为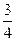 v=45千米/时.……………………3分
v=45千米/时.……………………3分
(2)y=45(x–2)=45x–90.……… ……………5分
……………5分
(3)630÷(60+45)=6.
当x=6时,y=180,所以点E的坐标为(6,180).……………………7分
点E表示当两车行驶了6小时时,在距离点C站180千米处相遇.……………8分
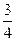 v千米/时,根据题意得
v千米/时,根据题意得9v +
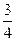 v ´2=630.……………………2分
v ´2=630.……………………2分解得v=60.
答:客车速度为60v千米/时,慢车的速度为
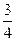 v=45千米/时.……………………3分
v=45千米/时.……………………3分(2)y=45(x–2)=45x–90.………
 ……………5分
……………5分(3)630÷(60+45)=6.
当x=6时,y=180,所以点E的坐标为(6,180).……………………7分
点E表示当两车行驶了6小时时,在距离点C站180千米处相遇.……………8分
略

练习册系列答案
相关题目
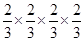 写成乘方的形式为________。
写成乘方的形式为________。
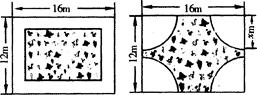





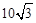 cm,其一个内角为60°,若纹饰的总长度L=5030 cm,当d=20时,则需要 个这样的菱形图案.
cm,其一个内角为60°,若纹饰的总长度L=5030 cm,当d=20时,则需要 个这样的菱形图案.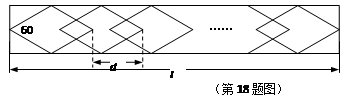

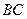 、
、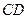 上有动点
上有动点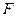 、
、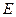 ,点
,点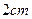 的速度,在线段
的速度,在线段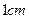 的速度,在线段
的速度,在线段 ,求y 关于t的函数关系式,并写出函数定义域;
,求y 关于t的函数关系式,并写出函数定义域;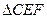 与
与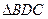 相似,求线段
相似,求线段 的长.
的长.