��Ŀ����
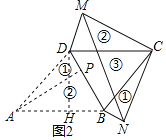
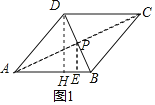
����Ŀ����ͼ1����һ��ABCD��ֽƬ�У�ABCD�����Ϊ6��DC��3����BCD��45������P��BD�ϵ�һ���㣨��P���B��D���غϣ����ֽ�����ֽƬ�ֱ���BD��AP�������飬����ͼ2��ע��ͼ2�еĢ٣����ǽ�ͼ1�еĢ٣��ڷ�ת���泯�ϣ���ƴ�Ӷ��ɵģ���ʾ����
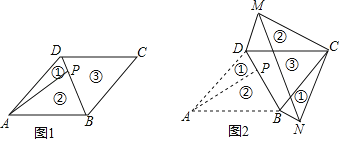
��1������P��BD���е�ʱ����AP�ij���
��2����̽��������P��BD��ʲôλ����ʱ��MN�ij���С������������Сֵ��
���𰸡���1��![]() ����2����AP��BDʱ��MN�ij���С��
����2����AP��BDʱ��MN�ij���С��![]()
��������
��1������AC��BD��P������ƽ���ı��ε����ʵõ�PD��PB������P��BD���е㣬��D��DH��AB��H��PE��AB��E�����������ε���λ�ߵ����ʵõ�PE��![]() DH��BE��
DH��BE��![]() BH��������֪�����õ�DH��2����ֱ�������μ��ɵõ����ۣ�
BH��������֪�����õ�DH��2����ֱ�������μ��ɵõ����ۣ�
��2��������ã�CM��CN��AP����MCD����PAB����NCB����PAD�����ǵõ���MCN��90������AP��BDʱ��MN�ij���С����D��DH��AB��H�����ݹ��ɶ����õ�BD��![]() ��
��![]() �����������ε������ʽ�õ�AP��
�����������ε������ʽ�õ�AP��![]() �����ݹ��ɶ������ɵõ����ۣ�
�����ݹ��ɶ������ɵõ����ۣ�
�⣺��1������AC��BD��P��
���ı���ABCD��ƽ���ı��Σ�
��PD��PB������P��BD���е㣬
��D��DH��AB��H��PE��AB��E��
��PE��DH��
��PE��![]() DH��BE��
DH��BE��![]() BH��
BH��
��ABCD�����Ϊ6��DC��3��
��DH��2��
��PE��1��
�ߡ�BCD��45����
���DAB��45����
��AH��DH��2��
��BH��1��
��HE��BE��![]() ��
��
��AE��![]() ��
��
��AP��![]() ��
��![]() ��
��
��2��������ã�CM��CN��AP����MCD����PAB����NCB����PAD��
���MCD+��NCB��45����
���MCN��90����
��AP��BDʱ��MN�ij���С��
��D��DH��AB��H��
�ɣ�1�����DH��2��BH��1
��BD��![]() ��
��![]() ��
��
��AP��BD��
��S��ABD��![]() ABDH��
ABDH��![]() BDAP��
BDAP��
��AP��![]() ��
��
��CM��CN��AP��![]() ��
��
��MN��![]() ��
��![]() ��
��
��MN������Сֵ��![]() ��
��