题目内容
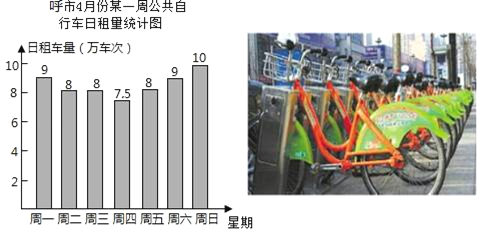
【题目】如图,直线y=x+3与x轴、y轴分别相交于A、C两点,过点B(6,0),E(0,﹣6)的直线上有一点P,满足∠PCA=135°.
(1)求证:四边形ACPB是平行四边形;
(2)求直线BE的解析式及点P的坐标.

【答案】(1)详见解析;(2)点P的坐标为(9,3).
【解析】
(1)利用一次函数图象上点的坐标特征可求出点A、C的坐标,进而可得出∠CAO=45°,结合∠PCA=135°可得出∠CAO+∠PCA=180°,利用“同旁内角互补,两直线平行”可得出AB∥CP,同理可求出∠ABE=45°=∠CAO,利用“内错角相等,两直线平行”可得出AC∥BP,再利用平行四边形的判定定理可证出四边形ACPB为平行四边形;
(2)由点B、E的坐标,利用待定系数法可求出直线BE的解析式,由AB∥CP可得出点P的纵坐标,再利用一次函数图象上点的坐标特征即可求出点P的坐标.
(1)∵直线y=x+3与x轴、y轴分别相交于A、C两点,
∴点A的坐标为(﹣3,0),点C的坐标为(0,3),
∴OA=OC.
∵∠AOC=90°,
∴∠CAO=45°.
∵∠PCA=135°,
∴∠CAO+∠PCA=180°,
∴AB∥CP.
∵点B的坐标为(6,0),点E的坐标为(0,﹣6),
∴OB=OE.
∵∠BOE=90°,
∴∠OBE=45°,
∴∠CAO=∠ABE=45°,
∴AC∥BP,
∴四边形ACPB为平行四边形.
(2)设直线BE的解析式为y=kx+b(k≠0),
将B(6,0)、E(0,﹣6)代入y=kx+b,得:
![]() ,解得:
,解得: ![]()
∴直线BE的解析式为y=x﹣6.
∵AB∥CP,
∴点P的纵坐标是3,
∴点P的坐标为(9,3).

练习册系列答案
相关题目